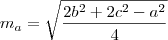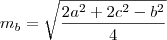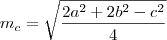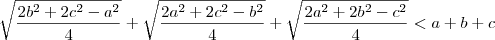por iclilima » Seg Jul 02, 2012 11:57
por iclilima » Seg Jul 02, 2012 11:57
Mostre que a soma das medidas das três medianas de um triângulo é menor que o perímetro desses triângulo.
-
iclilima
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jun 15, 2012 18:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Renato_RJ » Seg Jul 02, 2012 14:56
por Renato_RJ » Seg Jul 02, 2012 14:56
Boa tarde...
Acho que aqui cabe usar o Teorema de Stewart que diz que o valor de uma mediana relativa ao lado a, chamemos de
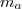
, é:
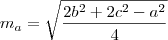
Agora façamos para os outros lados do triângulo, b e c, e teremos:
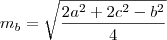
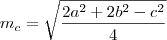
Somando as medianas temos:
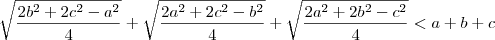
Agora é só resolver a inequação...
Espero que esteja tudo certinho...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Mediana]
por MarciaZardo » Sáb Jan 21, 2012 17:46
- 2 Respostas
- 1774 Exibições
- Última mensagem por MarciaZardo

Dom Jan 22, 2012 20:24
Estatística
-
- mediana
por alfabeta » Seg Mar 05, 2012 11:45
- 5 Respostas
- 3423 Exibições
- Última mensagem por LuizAquino

Seg Mar 05, 2012 22:45
Geometria Plana
-
- Mediana
por Pri Ferreira » Seg Abr 09, 2012 16:17
- 1 Respostas
- 1613 Exibições
- Última mensagem por LuizAquino

Ter Abr 10, 2012 20:55
Estatística
-
- Mediana e a Moda
por Walquiria » Dom Dez 18, 2011 12:14
- 0 Respostas
- 908 Exibições
- Última mensagem por Walquiria

Dom Dez 18, 2011 12:14
Estatística
-
- Mediana de classes
por ah001334 » Ter Mar 06, 2012 08:54
- 0 Respostas
- 1194 Exibições
- Última mensagem por ah001334

Ter Mar 06, 2012 08:54
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



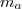 , é:
, é: