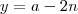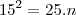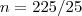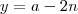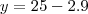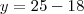por Matheus Lacombe O » Sex Fev 10, 2012 16:08
por Matheus Lacombe O » Sex Fev 10, 2012 16:08
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por LuizAquino » Dom Fev 12, 2012 15:09
por LuizAquino » Dom Fev 12, 2012 15:09
Matheus Lacombe O escreveu:Um retângulo ABCD - de medidas 20cm x 15 cm - é cortado por uma linha diagonal do ponto a ao ponto A ao ponto D, de forma a gerar dois novos triangulos retângulos. Cada um destes dois triângulos retângulos é cortado por uma linha de altura da hipotenusa até o ângulo reto.
- imagemqrb.jpg (6.36 KiB) Exibido 7747 vezes
- O exercicío pede as medidas x e y.
Matheus Lacombe O escreveu:Dúvida:
- Na resolução do livro "Matémática paratodos 8º série" o resultado desta questão (37, cap 1) aparece como sendo: x=1,8 e y=1,4. Tentei resolver fazendo a semelhança de triangulos lado-por-lado mas também não consegui. Onde foi que eu errei?
Você não errou. Considerando a figura, o gabarito correto é x = 9 e y = 7.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Matheus Lacombe O » Qua Fev 15, 2012 22:37
por Matheus Lacombe O » Qua Fev 15, 2012 22:37
Ufa! Obrigado. Acho que não estou maluco..
Abraços.
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Semelhança de Triângulos
 por vanessafey » Sáb Ago 27, 2011 23:50
por vanessafey » Sáb Ago 27, 2011 23:50
- 4 Respostas
- 8281 Exibições
- Última mensagem por vanessafey

Dom Ago 28, 2011 01:59
Geometria Plana
-
- Geometria Plana: Triângulos
por GuiBernardo » Qui Mar 02, 2017 18:49
- 0 Respostas
- 15943 Exibições
- Última mensagem por GuiBernardo

Qui Mar 02, 2017 18:49
Desafios Difíceis
-
- Geometria Plana, triângulos
 por FISMAQUI » Dom Abr 23, 2017 16:38
por FISMAQUI » Dom Abr 23, 2017 16:38
- 0 Respostas
- 11112 Exibições
- Última mensagem por FISMAQUI

Dom Abr 23, 2017 16:38
Geometria Plana
-
- [Geometria Plana] Triângulos isósceles
por DaviBahia » Sex Mar 22, 2013 13:23
- 2 Respostas
- 2884 Exibições
- Última mensagem por DaviBahia

Sáb Mar 23, 2013 06:16
Geometria Plana
-
- [Geometria Plana] Congruência de triângulos.
 por Debora Bruna » Seg Jan 11, 2016 18:20
por Debora Bruna » Seg Jan 11, 2016 18:20
- 1 Respostas
- 3354 Exibições
- Última mensagem por DanielFerreira

Dom Fev 07, 2016 14:52
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.