




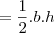
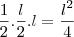
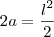
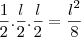
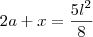
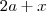 " do total da área do quadrado, que é
" do total da área do quadrado, que é 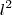 .
.

J Hugo escreveu:Na questão o lado quadrado e L dai em tao fasso pelo teorema de pitagoras para acha um dos lados do triangulo isosceles depois acho as outras
dai em tao acho a area do triangulo mais dai em diante nao acha o resultado certo...
se alguem soube pesso ajuda
Vlww


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

