É simples... eu faria por outra abordagem que iria facilitar (ou não) as coisas.
vamos pelo basico! voce precisa da area de um triangulo... a formula mais boba pra essa area é a famosa
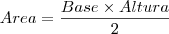
a base voce já sabe. é um lado do triangulo... agora a altura fica meio complicado... mas eu tenho um jeito!
- Na figura original construa um seguimento de reta que vá de D até E.
- Chame o angulo "D" de theta. (o angulo que esse seguimento faz com a base do triangulo)
- Agora, observe bem... a altura do triangulo será a progeção ortogonal desse seguimento na direção vertical. portanto

esse 2 corresponde ao tamanho do seguimento ED que é o raio da circunferencia!
Otimo... agora só falta descobrir o angulo theta! tente descobri-lo... eu já pensei em alguns jeitos aqui... mas tente descobri-los sosinho.
Dica, uma reta traçada do pto E até a base do triangulo perpendicularmente, cortará a base em duas partes iguais.


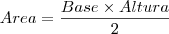
 esse 2 corresponde ao tamanho do seguimento ED que é o raio da circunferencia!
esse 2 corresponde ao tamanho do seguimento ED que é o raio da circunferencia!