 por ilovemat » Sex Abr 03, 2009 18:59
por ilovemat » Sex Abr 03, 2009 18:59
Oiii tenho uma dúvida em uma questão sobre circunferencia-->A profundidade da água de um porto pode ser modelada por uma função trigométrica devido as oscilaçoes das máres oceanicas. Se a profundidade da água em um porto da costa brasileira é dada pela fórmula D (t)+ 2,7 Cos(
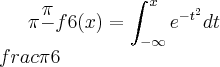
t) + 4,5 onde D é a profundidade da água em metros e t é medida em horas após a primeira maré alta do dia . Um comandante deve decidir o hr. de atracamento do seu navio nesse porto , optando entre atracar 7 hr. ou 11 hr. ´pós a primeira maré alta do dia . Em qual desses dois horários ele teria a maior profundidade da agua ?
meus calculos : D (t): 2,7 cos(
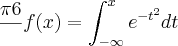
t} + 4,5
D(7)= 2,7 . cos 7.
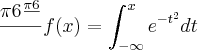
+ 4,5
agora eu não sei mas o que fazer alguem me ajuda ???
Obrigada
-
ilovemat
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Fev 19, 2009 16:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso de Administração
- Andamento: formado
 por Marcampucio » Sex Abr 03, 2009 20:53
por Marcampucio » Sex Abr 03, 2009 20:53
Não deu prá entender o que está escrito nos grafos matemáticos.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicio de quadrado, circunferencia e losango
 por Douglashsgomes » Seg Mai 05, 2014 19:56
por Douglashsgomes » Seg Mai 05, 2014 19:56
- 0 Respostas
- 716 Exibições
- Última mensagem por Douglashsgomes

Seg Mai 05, 2014 19:56
Geometria Plana
-
- Dúvida em Circunferência
por thiagohcacique » Qua Abr 17, 2013 19:07
- 3 Respostas
- 1584 Exibições
- Última mensagem por young_jedi

Qui Abr 18, 2013 20:06
Geometria Analítica
-
- Geometria Analitica - Circunferência - Duvida
por PiterPaulo » Sáb Mai 11, 2013 21:12
- 0 Respostas
- 1446 Exibições
- Última mensagem por PiterPaulo

Sáb Mai 11, 2013 21:12
Geometria Analítica
-
- [circunferência] Questão de reta secante a circunferência
por danielleecb » Qui Jun 07, 2012 23:26
- 1 Respostas
- 1879 Exibições
- Última mensagem por MarceloFantini

Sex Jun 08, 2012 12:24
Geometria Analítica
-
- Dúvida em exercício de PAG!
 por Fernanda » Qui Jul 03, 2008 18:20
por Fernanda » Qui Jul 03, 2008 18:20
- 11 Respostas
- 10121 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:01
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
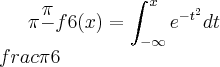 t) + 4,5 onde D é a profundidade da água em metros e t é medida em horas após a primeira maré alta do dia . Um comandante deve decidir o hr. de atracamento do seu navio nesse porto , optando entre atracar 7 hr. ou 11 hr. ´pós a primeira maré alta do dia . Em qual desses dois horários ele teria a maior profundidade da agua ?
t) + 4,5 onde D é a profundidade da água em metros e t é medida em horas após a primeira maré alta do dia . Um comandante deve decidir o hr. de atracamento do seu navio nesse porto , optando entre atracar 7 hr. ou 11 hr. ´pós a primeira maré alta do dia . Em qual desses dois horários ele teria a maior profundidade da agua ?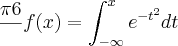 t} + 4,5
t} + 4,5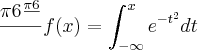 + 4,5
+ 4,5



 .
.



