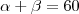por Sergio Crisostomo » Sáb Jun 18, 2011 12:54
por Sergio Crisostomo » Sáb Jun 18, 2011 12:54
Bom dia
Gostaria que vocês me ajudassem a resolver este problema:
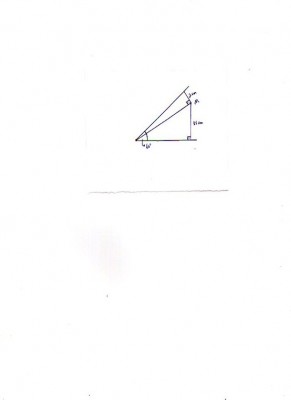
Um ponto M está dentro da região limitada por um ângulo de 60º, distando 2cm de um lado e 11cm do outro lado. Determine sua distância ao vértice do ângulo.
Obs.: Tentei usar o teorema de pitágoras nos dois triângulos, formado entre o vértice, o ponto M e outro lado, todavia não obtive êxito, com resolverei este problema?
Obrigado pela atenção
- Anexos
-
-
Sergio Crisostomo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jun 18, 2011 12:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por FilipeCaceres » Sáb Jun 18, 2011 14:30
por FilipeCaceres » Sáb Jun 18, 2011 14:30
Tente fazer isto, acredito que saia a resposta.
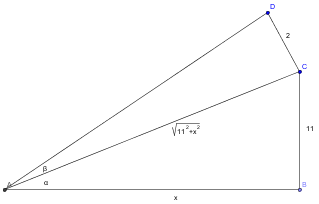
- triangulo.png (4.34 KiB) Exibido 1458 vezes
Agora faça,
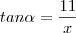
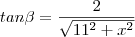
Logo,
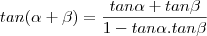
, onde
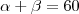
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Sergio Crisostomo » Sáb Jun 18, 2011 23:55
por Sergio Crisostomo » Sáb Jun 18, 2011 23:55
Fiz esta pergunta mais graças a Deus consegui responder, agradeço também ao colega que mandou a primeira resposta, no entanto serve para que outros tirem também suas dúvidas.
Segue em anexo a minha resolução.
Felicidade a todos que Deus vos abençoe e bons estudos.
Sérgio Crisóstomo
- Anexos
-
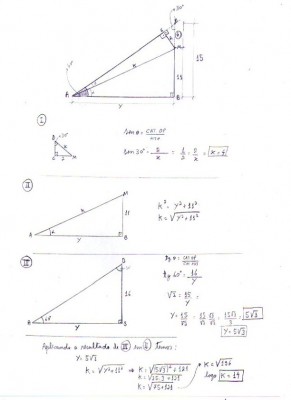
-
Sergio Crisostomo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jun 18, 2011 12:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8726 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4721 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4829 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2542 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3683 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


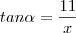
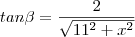
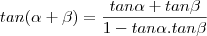 , onde
, onde