geometria plana

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

geometria plana

Regras do fórum
Responder

geometria plana

Mensagempor fttofolo » Sáb Mai 28, 2011 18:42

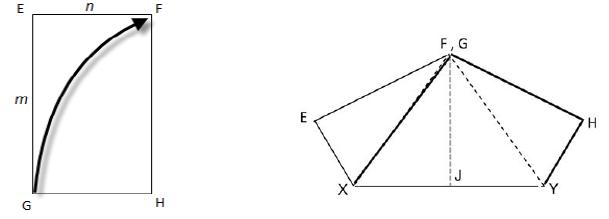
O retângulo EFGH mostrado na figura possui dimensões m e n e foi dobrado, de modo que o vértice G foi colocado
sobre o vértice F. O ponto J é o pé da altura do triângulo FXY, relativa ao lado XY.

Se os triângulos EFX, FXJ, FJY e HFY forem congruentes, pode-se afirmar que a razão \frac{m}{n} entre as duas dimensões do retângulo é:

a)\sqrt[]{2}
b)3/2
c)\sqrt[]{3}
d) 2
e) 2\sqrt[]{2}
Anexos
ex 32.JPG
ex 32.JPG (10.72 KiB) Exibido 840 vezes
fttofolo
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 26
Registrado em: Sex Nov 19, 2010 10:15
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo
Responder

Voltar para Geometria Plana

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum