Num referencial ortonormado está representado uma pirâmide reta, quadrangular regular de vértice V (3,3,0) e base [ABCD].
- A altura da pirâmide é de 2,5 cm
- A base da pirâmide é paralela ao plano XOY
- O vértice D pertence ao eixo OZ
- O vértice A pertence ao plano XOZ
(um pouco mal desenhado mas dá para perceber)

1 - Identifique as coordenadas dos pontos D, B, C e A.
D (0;0;2,5) C (0;6;2,5)
B (6;6;2,5) A (6;0;2,5)
2 - Escreva a equação do plano ABV.
Sabendo que a equação do plano é dada por:
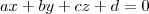
Para determinar a equação temos que descobrir o vetor. É isso certo?
3 - Calcule A
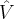 B (em graus e minutos).
B (em graus e minutos).Aqui a única coisa que sei é AB=6 certo?
Tenho algumas dúvidas aqui.
4 - Determine o volume da pirâmide.
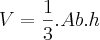

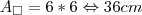
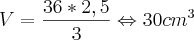


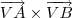
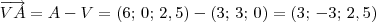
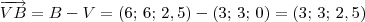
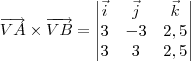
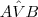 , use a relação abaixo:
, use a relação abaixo: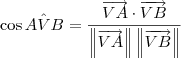
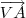 e
e 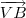 você já calculou no quesito anterior.
você já calculou no quesito anterior.
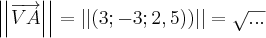
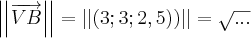
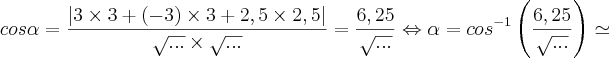
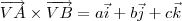
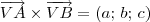
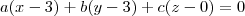
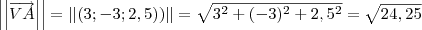
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)