 por adauto martins » Sex Dez 06, 2019 12:36
por adauto martins » Sex Dez 06, 2019 12:36
(ITA-exame 1957)
a que distancia do vertice devemos cortar um cone de revoluçao,por um plano paralelo a base,de modo que o volume do cone
destacada seja 1/8 do volume do primeiro cone?
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Dez 06, 2019 13:06
por adauto martins » Sex Dez 06, 2019 13:06
soluçao
pelos dados do problema,teremos
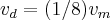
´
onde
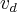
volume do cone destacado,
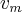
volume do cone maior.éntao
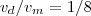
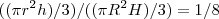


por semélhança de triangulos retangulos obtidos pelas alturas e raios dos triangulos inseridos no cone,teremos´
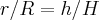
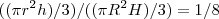

´

´
substituindo (**) em (*),teremos
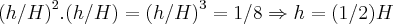
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



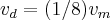 ´
´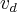 volume do cone destacado,
volume do cone destacado,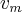 volume do cone maior.éntao
volume do cone maior.éntao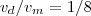
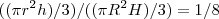


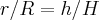
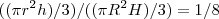
 ´
´ ´
´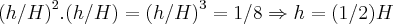


 .
.
 :
: