Dado um prisma hexagonal regular, sabendo que sua altura mede 3 cm e que sua área lateral é o dobro da área de sua base. O volume desse prisma, em centímetros cúbicos, é:
nem sei por onde começar, alguem me ajuda???



 ) é o triplo da área da base, pois:
) é o triplo da área da base, pois: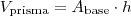
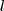

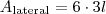
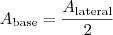

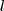 e termine com:
e termine com: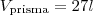
Ao calcular, note os 6 triângulos equiláteros que constituem a base hexagonal regular.
Obtenha a área da base que é 6 vezes a área de cada triângulo deste.
Utilize esta equação dada no enunciado e encontrará o valor de:

Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

