Olá
Ananda!
Acho importante começarmos discutindo um plano para resolução que servirá como referência para outros problemas.
Pede-se para calcular o
volume do segmento cilíndrico que é reto.
Aqui, o termo "reto" nos diz que o ângulo entre a base circular e a prolongação do cilindro é de
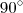
.
Pois bem, a chave para a resolução é partir dos conceitos mais elementares.
Não queira resolver o exercício diretamente.
Inicie o raciocício pelo que se pede e em seguida, tente construir os passos anteriores que levam até lá.
Vamos nomear alguns pontos no círculo base para facilitar a identificação.
Veja:
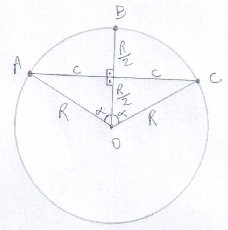
- circulo.jpg (10.86 KiB) Exibido 9535 vezes
Considerando o conceito elementar de
volume do segmento de interesse, o que precisamos?
Como é reto, apenas precisamos da área da base deste sólido superior, pois o comprimento já temos.
Depois então, calculamos o
volume com o produto área da base pelo comprimento que é
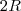
.
Identificando esta base:
Veja que a base deste sólido é
, precisamos calcular esta área.
Considere que você tem um sub-problema agora.
Como calcular esta área
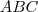
?
A idéia é calcular áreas de regiões mais simples e obter esta por diferença.
Por exemplo, é fácil calcular a área do região
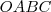
.
Após, repare que se subtraírmos a área do triângulo
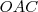
, obteremos a área da região que queremos
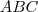
. Vamos fazer assim!
Antes, precisamos daquele ângulo

.
E para obtê-lo, vamos calcular

, por Pitágoras.
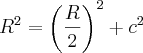
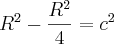
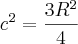
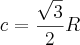
E para

, utilizaremos seno:
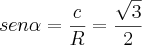

Agora, vamos voltar para nosso plano.
Calculando a área da região
:
Podemos fazer uma regra de três.
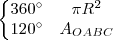
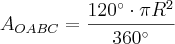
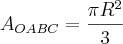
Pronto, mais um passo.
Na seqüência, a área do triângulo
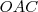
:
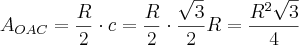
Agora que já temos as áreas intermediárias que precisávamos, vamos enfim obter a área da região
:
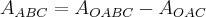
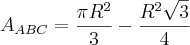
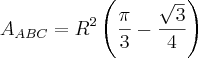
E finalmente, o
volume que precisamos:
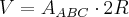
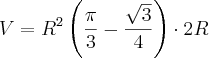
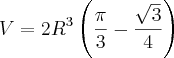
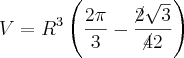
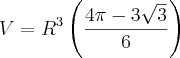 Ananda
Ananda, resumindo, não se preocupe em querer resolver os problemas de uma só vez, ou, se não conseguir construir imediatamente um caminho para a resolução.
Lembre-se: comece procurando "algo" que falta para se obter a resposta. Em seguida, perceberá que para antes conseguir este "algo", precisará calcular um "algo2" etc. Assim, você construirá os passos que levarão à resolução final.
Espero ter ajudado!
Bons estudos.
![\frac{R^3(4\pi-3\sqrt[]{3)}}{6} \frac{R^3(4\pi-3\sqrt[]{3)}}{6}](/latexrender/pictures/0f48e93063706f1725e85f3af9cbc788.png)


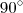 .
.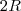 .
.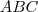 , precisamos calcular esta área.
, precisamos calcular esta área.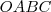 .
.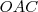 , obteremos a área da região que queremos
, obteremos a área da região que queremos  .
. , por Pitágoras.
, por Pitágoras.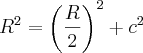
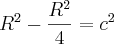
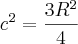
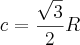
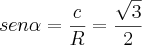

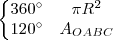
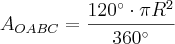
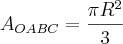
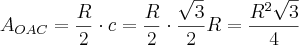
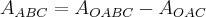
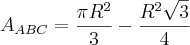
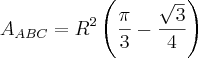
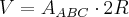
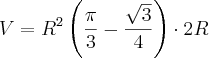
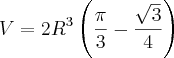
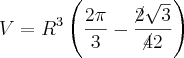
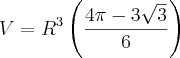



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.