 por rochadapesada » Dom Abr 14, 2013 17:49
por rochadapesada » Dom Abr 14, 2013 17:49
Essa é outra questão de rotação que não bate o valor... Eu sei que, com a rotação, irá surgir um tronco de cone, ai eu termino esse tronco, colocando um cone em cima dele para fazer: o volume do cone maior - volume do cone menor = volume do tronco, mas não acho a resposta:
Um trapézio isósceles cujas bases medem 2 cm e 4 cm, respectivamente, e cuja altura é de 1 cm, sofre uma rotação de 360 graus em torno da base maior, gerando assim um sólido. O volume desse sólido é:
a)


b)
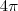

c)
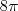

d)


e)
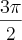

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Seg Abr 15, 2013 21:42
por young_jedi » Seg Abr 15, 2013 21:42
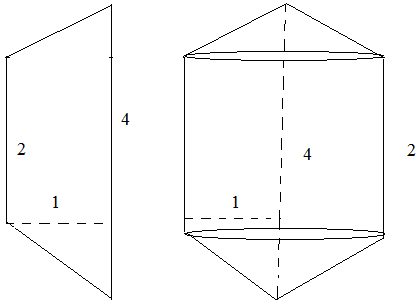
- trap_rev.png (4.31 KiB) Exibido 6697 vezes
analisando a figura temos o trapezio e o solido de revolução gerado veja que ele pode ser decomposto em cilindro de raio 1 e altura 2 e em dois cones de raio de base 1 e altura 1, tente calcular
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Ter Abr 16, 2013 18:07
por rochadapesada » Ter Abr 16, 2013 18:07
Obrigado cara
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial] Rotação de um triângulo
 por rochadapesada » Dom Abr 14, 2013 17:40
por rochadapesada » Dom Abr 14, 2013 17:40
- 3 Respostas
- 4001 Exibições
- Última mensagem por rochadapesada

Ter Abr 16, 2013 17:56
Geometria Espacial
-
- [Geometria] Altura de um trapézio isósceles.
 por Biliyorum » Qua Out 05, 2011 16:01
por Biliyorum » Qua Out 05, 2011 16:01
- 0 Respostas
- 1658 Exibições
- Última mensagem por Biliyorum

Qua Out 05, 2011 16:01
Geometria Plana
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11738 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2857 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6154 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


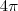

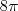



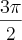




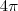

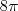



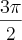




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.