 por marina jose » Seg Fev 20, 2012 10:41
por marina jose » Seg Fev 20, 2012 10:41
Como faço para determinar o numero de diagonais sem contar as diagonais de cada face??? !!!!
-
marina jose
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 17, 2012 17:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por LuizAquino » Seg Fev 20, 2012 12:43
por LuizAquino » Seg Fev 20, 2012 12:43
marina jose escreveu:Como faço para determinar o numero de diagonais sem contar as diagonais de cada face???
Suponha que o poliedro tenha
v vértices e
a arestas. Além disso, suponha que contando todas as diagonais das faces, obtemos um total de
d diagonais.
Para calcular o número de diagonais sem considerar aquelas que estão sobre as faces, basta efetuar a operação:
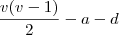
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vanessa_mat » Qua Fev 22, 2012 17:40
por vanessa_mat » Qua Fev 22, 2012 17:40
LuizAquino escreveu:marina jose escreveu:Como faço para determinar o numero de diagonais sem contar as diagonais de cada face???
Suponha que o poliedro tenha
v vértices e
a arestas. Além disso, suponha que contando todas as diagonais das faces, obtemos um total de
d diagonais.
Para calcular o número de diagonais sem considerar aquelas que estão sobre as faces, basta efetuar a operação:
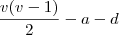
Estou tentando entender o problema das diagonais, mas essa fórmula, não conhecia...como faço para conseguir entender o problema??
-
vanessa_mat
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Seg Nov 21, 2011 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qua Fev 22, 2012 22:36
por LuizAquino » Qua Fev 22, 2012 22:36
vanessa_mat escreveu:Estou tentando entender o problema das diagonais, mas essa fórmula, não conhecia...como faço para conseguir entender o problema??
DicaNote que escolhendo-se dois vértices distintos, podemos formar um dos três elementos:
(i) uma aresta;
(ii) uma diagonal sobre a face;
(iii) uma diagonal fora da face.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11742 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2859 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6159 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3169 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4213 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 .
.



