Volume de uma caixa retangular

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Volume de uma caixa retangular

Regras do fórum
Responder

Volume de uma caixa retangular

Mensagempor Andreza » Sáb Nov 12, 2011 10:02

Considere uma caixa d’água retangular, de base quadrada. De um dos vértices da base, A, marcamos AB=2m sobre a aresta lateral que contém A. Escolha qualquer uma das faces laterais que não contém AB e marque sobre ela o ponto P, interseção das diagonais dessa face. A medida de BP é 10m. BP tem uma inclinação de 30° em relação à base da caixa. Qual o volume da caixa?

Eu já tentei nao consegui nem o desenho coerente.
Qualquer dica é bem vinda.
Obrigada.
Aguardo resposta.
Andreza
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 100
Registrado em: Sáb Out 22, 2011 11:10
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Licenc. Plena Matemática
Andamento: formado
Voltar ao topo

Re: Volume de uma caixa retangular

Mensagempor LuizAquino » Qui Nov 17, 2011 22:16

Andreza escreveu:Considere uma caixa d’água retangular, de base quadrada. De um dos vértices da base, A, marcamos AB=2m sobre a aresta lateral que contém A. Escolha qualquer uma das faces laterais que não contém AB e marque sobre ela o ponto P, interseção das diagonais dessa face. A medida de BP é 10m. BP tem uma inclinação de 30° em relação à base da caixa. Qual o volume da caixa?


Andreza escreveu:Eu já tentei nao consegui nem o desenho coerente.


A figura abaixo (fora de escala) ilustra o exercício. Considere que os lados da base medem a.

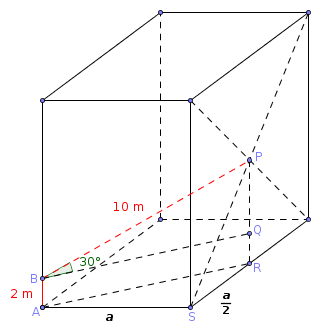
caixa.png
caixa.png (13.13 KiB) Exibido 1674 vezes



Andreza escreveu:Qualquer dica é bem vinda.
Obrigada.
Aguardo resposta.


Note que:
  • BQP é um triângulo retângulo;
  • BQ é paralelo a AR;
  • ASR é um triângulo retângulo;
  • PR é equivalente a metade da altura da caixa.

Agora tente resolver o exercício.
professoraquino.com.br | youtube.com/LCMAquino | @lcmaquino

"Sem esforço, não há ganho."
Dito popular.
Avatar do usuário
LuizAquino
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 2654
Registrado em: Sex Jan 21, 2011 09:11
Localização: Teófilo Otoni - MG
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Mestrado - Modelagem Computacional
Andamento: formado
Voltar ao topo
Responder

Voltar para Geometria Espacial

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum