 por Thata » Sex Out 07, 2011 12:27
por Thata » Sex Out 07, 2011 12:27
Por favor, me ajudar a resolver a seguinte questão:
Um tanque cilindrico, cheio de combustível, de raio igual a 1 m e altura igual a 4m ao ser suspenso por um cabo de aço fixado no ponto P, inclinou-se até a posição mostrada na figura,
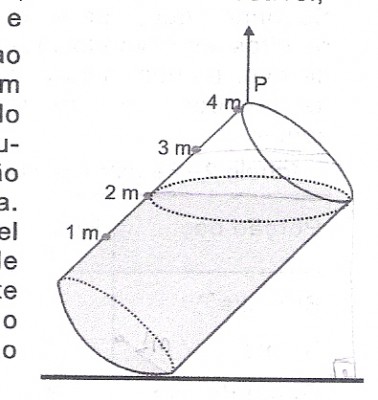
- Imagem para resolução da questão.
parte do combustível foi derramada, de modo que o restante ficou nivelado como se vê na figura. A quantidade de combustível que restou no tanque foi?
Eu tentei fazer, porém a resposta não bate com o gabarito. Eu fiz o seguinte: achei o volume do cilindro quando este estava reto, o que deu igual a 12,56 metros cúbico. Quando o cilindro ficou inclinado a parte vazia se assemelha a um cone, daí eu achei o volume deste cone que daria igual a 2,09 metros cúbicos. Assim, reduzindo o volume do cilindro (quando reto) do volume do cone (parte vazia) eu encontraria a quantidade de combustível que sobrou que, na minha resposta daria 10,47 metros cúbicos. Porém o gabarito é 9,42 metros cúbico. Aí eu pergunto: onde é que eu estou errando??
P.S: A imagem segue em anexo.
Att. Obrigada.
-
Thata
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 07, 2011 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por renatoslmb » Sáb Dez 31, 2011 11:43
por renatoslmb » Sáb Dez 31, 2011 11:43
e simples a parte vazia não é um cone pois duas de suas faces laterais uma e circunferência e outra elipse
e muito simples de se resolver repare que a parte que tem combustível e um tronco de tronco para se calcular o volume e simples
Abase x h onde a altura e a soma das laterais do tronco dividido por 2
então fica assim 3,14 x 1^2 x (2+4)/2= 9,42 m cúbicos
se tiver msn min add la
renatolorenco@hotmail.com
-
renatoslmb
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Dez 31, 2011 11:24
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11743 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2860 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6160 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3169 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4213 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.