hevhoram, vc chutou longe..
não tem base o que vc tentou...
para resolver, precisaremos trabalhar com duas formulas tradicionaias sobre cincunferencia
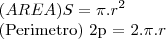
Sabendo disso, teremos varias etapas (perceba q estamos lidando com 02 circulos):
1- Calcular o perimetro do circulo menor (base do chapeu que term o raio = 15)
2- esse perimetro passará a ser, uma fração do perimetro do circulo maior (o chapeu propriamente dito, quando está planificado)
3- descobrirmos qual a razão entre os 02 perimetros
4- calcular a area total do circulo maior,
5- e multiplicar pela razão
6- multiplicar por 40 chapeus (e converter para m²)
01 (Perimetro do circ menor)
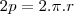
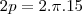
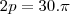
cm²
02 (Perimetro do circ maior)
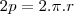
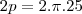
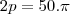
cm²
03 A razão é de
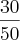
ou

ou 0,6
04 Area Total do circulo maior
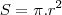
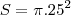
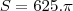
cm²
05 multiplicando pela razão, obtemos a resposta (para 01 chapéu)

.
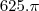
cm²
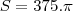
cm²
06 para 40 chapéus:
40 .
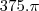
cm²
=

cm²
= 47100 cm²
= 4,71 m²
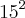 depois multipliquei por 40 mas não deu o resultado. como proceder?
depois multipliquei por 40 mas não deu o resultado. como proceder?

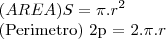
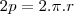
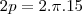
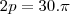 cm²
cm²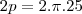
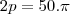 cm²
cm²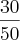 ou
ou  ou 0,6
ou 0,6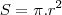
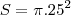
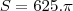 cm²
cm²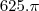 cm²
cm² 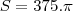 cm²
cm²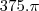 cm²
cm²  cm²
cm²