59. Um reservatório de gás é feito de um cilindro com um hemisfério em cima, como mostra a figura.

O diâmetro do reservatório é de 12m, e a altura total é de 10m. Então, o volume desse reservatório é de, aproximadamente:
resposta: 900 m³
Eu tentei assim, vê se cheguei perto.
Volume da semi-esfera:
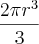 =
= 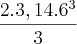
Volume do cilindro:
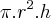 = 3,14.6².5
= 3,14.6².5Vol. semi-esfera + vol. do cilindro = 1017,36 (resposta errada).
Eu não sabia o que fazer com a altura e chutei a altura do cilindro 5 a metade do reservatório, mas acho que a altura tá errada porque não encontrei a resposta certa.
Agradeço a algum dos amigo que puder ajudar.



