 por renataf » Seg Nov 29, 2010 17:38
por renataf » Seg Nov 29, 2010 17:38
Uma indústria de cosméticos deseja embalar sabonetes esféricos de raio 3cm. A embalagem deverá ter formato cilíndrico, de forma a acondicionar 3 sabonetes, como mostra a figura (vista superior da embalagem aberta). A medida do raio e a altura da embalagem, em cm, deverão ser de aproximadamente: (
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
=1,73)
A)6,73 e 3
B)6,73 e 6
C)6,46 e 3
D)3,46 e 6
E)6,46 e 6
http://www.supletivounicanto.com.br/docs/cd/Matem%E1tica/3%B0%20ano/08-esfera.pdf Exercício 6.
A resposta é a D, mas eu fiz e não consigo chegar em 6,46.
Minha resolução.
Volume das esferas:


Resolvendo vai ficar:
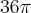
(esse é o volume de 1 sabonete como são 3) fica:

Aí o volume do cilindro:


(a altura vai ser = ao diâmetro da esfera portanto vai ser 6)

( o raio, pelas minhas contas vai ser assim: se eu fizer um triangulo equilátero q passe pelo cento da figura, a altura desse triangulo derá o raio do cilindro)
![\pi x \left({\frac{L\sqrt[]{3}}{2}} \right)^{2} x 6 \pi x \left({\frac{L\sqrt[]{3}}{2}} \right)^{2} x 6](/latexrender/pictures/2b954b871c9b3fd640fb2c4fa5239c58.png)
= Volume cilindro

=

Resolvendo:

L=4,90
Aí, como o raio é igual a altura do triangulo equilátero eu subtitui na formula. Ficando:
![r= \frac{L\sqrt[]{3}}{2} r= \frac{L\sqrt[]{3}}{2}](/latexrender/pictures/1857a0e654f967f463c551531c9f0882.png)

r=4,24
Não sei onde estou errando.
-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Seg Nov 29, 2010 18:01
por Elcioschin » Seg Nov 29, 2010 18:01
Use o desenho mostrado
Seja r = 3 o raio de cada esfera e R o raio da caixa cilíndrica
Uma os centros das 3 esferas: o resultado é um triângulo equilátero de lado L = 2r
A altura deste triângulo vale: h = L*cos30º ----> h = (2r)*V3/2 ----> h = r*V3
Una agora o centro O do cilindro ao centro C de uma das esferas e prolongue até alcançar a parede do cilindro no ponto P
OC = (2/3)*h ----> OC = (2/3)*r*V3 ----> OC = (2*V3/3)*r
CP = r
R = OP ----> R = OC + CP ----> R = (2*V3/3)*r + r ----> R = (2*V3/3 + 1)*r ----> R = (2*V3/3 + 1)*3 ----> R ~= 6,46 cm
A altura do cilindro é igual ao diâmetro das esferas ----> h = 2r ----> h = 6 cm
Obs.: Suas alternativas estão diferentes do desenho
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por renataf » Seg Nov 29, 2010 18:55
por renataf » Seg Nov 29, 2010 18:55
Um pouco confuso, mas consegui entender. Obrigada!

-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 9586 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- Esfera
por Pri Ferreira » Ter Mai 08, 2012 21:49
- 1 Respostas
- 2132 Exibições
- Última mensagem por Guill

Seg Mai 14, 2012 00:02
Geometria Espacial
-
- Esfera
por Fernandobertolaccini » Sex Mai 02, 2014 09:36
- 0 Respostas
- 1952 Exibições
- Última mensagem por Fernandobertolaccini

Sex Mai 02, 2014 09:36
Geometria Espacial
-
- questoes de esfera
por camilalindynha » Ter Dez 11, 2007 09:12
- 1 Respostas
- 11238 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 12:26
Geometria Espacial
-
- Esfera e cone
 por Ananda » Sex Abr 04, 2008 15:21
por Ananda » Sex Abr 04, 2008 15:21
- 4 Respostas
- 8369 Exibições
- Última mensagem por admin

Sex Abr 04, 2008 17:49
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) =1,73)
=1,73)

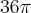 (esse é o volume de 1 sabonete como são 3) fica:
(esse é o volume de 1 sabonete como são 3) fica: 

 (a altura vai ser = ao diâmetro da esfera portanto vai ser 6)
(a altura vai ser = ao diâmetro da esfera portanto vai ser 6) ( o raio, pelas minhas contas vai ser assim: se eu fizer um triangulo equilátero q passe pelo cento da figura, a altura desse triangulo derá o raio do cilindro)
( o raio, pelas minhas contas vai ser assim: se eu fizer um triangulo equilátero q passe pelo cento da figura, a altura desse triangulo derá o raio do cilindro)![\pi x \left({\frac{L\sqrt[]{3}}{2}} \right)^{2} x 6 \pi x \left({\frac{L\sqrt[]{3}}{2}} \right)^{2} x 6](/latexrender/pictures/2b954b871c9b3fd640fb2c4fa5239c58.png) = Volume cilindro
= Volume cilindro =
=

![r= \frac{L\sqrt[]{3}}{2} r= \frac{L\sqrt[]{3}}{2}](/latexrender/pictures/1857a0e654f967f463c551531c9f0882.png)






 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.