soluçao
aqui temos uma piramide regular(base de poligonos regulares,ou seja mesma medida dos lados),em nosso caso um quadrado.
mas a piramide nao pode ser reta(caso do ponto da base da altura estar no centro do poligono),pois aresta lateral e menor que 2m,ponto de encontro das diagonais.vamos a soluçao
o volume de uma piramide é dado por
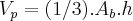
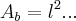
onde
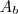 area
area da base,
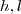
altura e base respectivamente...
vamos calcular
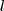
as diagonais se interceptam ao meio,logo teremos
triagulos-retangulos isosceles de lados iguais a 2m...tomemos um triangulo e usando pitagoras teremos...
![{l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8... {l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8...](/latexrender/pictures/083829b50084756195cd8f50a988d3db.png)
agora vamos calcular a altura h...como dito,a piramide é nao reta,logo a base da altura nao esta no centro do quadrado,pois a aresta lateral de medida 1,5 é menor que 2...mas continua na reta que liga os pontos medios de lados opostos(mostre isso,aqui é usar o centro de gravidade da piramide...)
a piramide tera duas faces laterais iguais e duas outras faces diferentes...as duas faces iguais sao triangulos retangulos,mostra-se usando o criterio de semelhança LAL,sao as faces que contem a aresta lateral de 1,5...
tomemos uma dessas faces,teremos entao um tringulo-retangulo de medidas 1.5,2,x...x a determinar...usando pitagoas teremos
![x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)} x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)}](/latexrender/pictures/d743c3cca872f22a3b3550cd790abbc1.png)
x é o segmento dessa face,que une o vertice ao lado e perpendicular a esse...
tomemos o triangulo constituido por x,h,e o ponto da base da altura que sera a metade do ponto medio do lado do quadrado,que mede
![\sqrt[]{2}... \sqrt[]{2}...](/latexrender/pictures/92f8b9302ed14c65b3537c898831d81b.png)
logo,usando pitagoras teremos
![x=\sqrt[]{23/4}=\sqrt[]{23}/2... x=\sqrt[]{23/4}=\sqrt[]{23}/2...](/latexrender/pictures/1688a6d3c08f3956f20c01f7a02228a8.png)
![{x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}... {x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}...](/latexrender/pictures/b027b7357980bbe3ccde5df2916ca2f5.png)



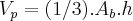
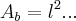
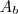 area da base,
area da base,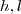 altura e base respectivamente...
altura e base respectivamente...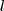
![{l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8... {l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8...](/latexrender/pictures/083829b50084756195cd8f50a988d3db.png)
![x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)} x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)}](/latexrender/pictures/d743c3cca872f22a3b3550cd790abbc1.png)
![\sqrt[]{2}... \sqrt[]{2}...](/latexrender/pictures/92f8b9302ed14c65b3537c898831d81b.png)
![x=\sqrt[]{23/4}=\sqrt[]{23}/2... x=\sqrt[]{23/4}=\sqrt[]{23}/2...](/latexrender/pictures/1688a6d3c08f3956f20c01f7a02228a8.png)
![{x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}... {x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}...](/latexrender/pictures/b027b7357980bbe3ccde5df2916ca2f5.png)

![x=\sqrt[]{23}/2 x=\sqrt[]{23}/2](/latexrender/pictures/e47a516db990fda27f146e259d02a562.png) nao é o segmento que une o vertice ao lado do quadrado,perpendicular a esse,e sim a outra aresta lateral...entao,vamos calcular esse segmento(chamaremos de y...).usando o criterio de semelhança LAL,teremos
nao é o segmento que une o vertice ao lado do quadrado,perpendicular a esse,e sim a outra aresta lateral...entao,vamos calcular esse segmento(chamaremos de y...).usando o criterio de semelhança LAL,teremos![y/(\sqrt[]{23}/2)=1.5/2\sqrt[]{2}=(3/2)/2\sqrt[]{2}
\Rightarrow y=(3/8).\sqrt[]{23}... y/(\sqrt[]{23}/2)=1.5/2\sqrt[]{2}=(3/2)/2\sqrt[]{2}
\Rightarrow y=(3/8).\sqrt[]{23}...](/latexrender/pictures/15d76a347d6a0cd869d1f16e67728837.png)
![y=(3/8).\sqrt[]{23},l=\sqrt[]{2},h y=(3/8).\sqrt[]{23},l=\sqrt[]{2},h](/latexrender/pictures/6a3f3a5d7b47bdf65ed548391b881fd7.png) ,determinaremos h.usando pitagoras teremos
,determinaremos h.usando pitagoras teremos![h=\sqrt[]{{((3/8).\sqrt[]{23}})^{2}-{(\sqrt[]{2}})^{2}}
h=\sqrt[]{79/64}=\sqrt[]{79}/8 h=\sqrt[]{{((3/8).\sqrt[]{23}})^{2}-{(\sqrt[]{2}})^{2}}
h=\sqrt[]{79/64}=\sqrt[]{79}/8](/latexrender/pictures/05e613c5308f861564624f6c3d72abb6.png)
![{V}_{p}=(1/3).8.(\sqrt[]{79}/8)=\sqrt[]{79}/3... {V}_{p}=(1/3).8.(\sqrt[]{79}/8)=\sqrt[]{79}/3...](/latexrender/pictures/21229594f32ed84b841692a7218d39a6.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.