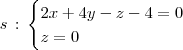manuel_pato1 escreveu:Sejam a reta r e o plano

, dados por:
r: y=2x-3 / z=-x + 2 e

: 2x+ 4y- z - 4=0
a - O ponto de interseção de r com o plano xOz
c - equações da reta interseção de

com o plano xOy
manuel_pato1 escreveu:**Na letra a, a resposta é: (3/2 , 0 , 1/2)
Essa resposta é exatamente o ponto que está na reta , pois quando a parametrizei , encontrei que x= 3/2 + t , y=2t, 1/1 -t.
Só que aí vem a minha dúvida. não entendi pq é o mesmo ponto da reta. Eu teria que ter a visão de que por ela apresentar um ponto nulo somente em y quer dizer que ela está no plano xOz?
Primeiro, uma observação: as equações paramétricas que você encontrou seriam x= 3/2 + t, y = 2t e z = 1/2 - t (note que você escreveu "1/1 - t" no final).
Agora pense um pouco: se o ponto está na
interseção de r com o plano xOz, então é claro que esse ponto está ao mesmo tempo nessa reta e nesse plano.
Você já sabe que a equação do plano xOz é dada por y = 0. Portanto, todos os pontos desse plano possuem o formato (k, 0, m), sendo k e m escalares quaisquer.
Por outro lado, você obteve uma parametrização da reta r de tal modo que identificou que ela passa pelo ponto (3/2, 0, 1/2). Já que esse ponto tem o formato dos pontos no plano xOz, você já pode afirmar que ele também faz parte desse plano. Portanto, esse ponto está na interseção de r e xOz.
A questão aqui é que você achou uma parametrização conveniente, que já fornece diretamente o ponto que está na interseção. Mas você poderia ter achado outra parametrização que não acontece isso. Por exemplo, outras equações paramétricas para r seriam x = t, y = -3 + 2t e z = 2 - t. Nesse caso, sabemos imediatamente que a reta r passa pelo ponto (0, -3, 2). Mas esse ponto não pode estar no plano xOz. Para achar outro ponto de r que esteja nesse plano, basta lembrar que a equação do plano é y = 0. Sendo assim, teremos -3 + 2t = 0, de onde concluímos que em t = 3/2 a reta intercepta o plano. Substituindo esse valor de t nas equações paramétricas, obtemos x = 3/2, y = 0 e z = 1/2.
manuel_pato1 escreveu:***A letra c, eu realmente não sei começar =S , a resposta dela é: y= -1/2x +1 , z=0
Você já tem que a equação de

é dada por 2x + 4y - z - 4 = 0. Por outro lado, você sabe que o plano xOy tem equação z = 0. Portanto, a reta de interseção entre esses planos (que aqui chamarei de s) será dada por:
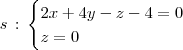
Tente concluir o item c) considerando essas informações.
 , dados por:
, dados por: : 2x+ 4y- z - 4=0
: 2x+ 4y- z - 4=0 com o plano xOy
com o plano xOy