-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480197 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539387 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503275 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 727103 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2163280 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por jennakusterbeck » Qui Set 20, 2012 13:52
por jennakusterbeck » Qui Set 20, 2012 13:52
r: x = 2t
y = 1 - t
z = 2 + t
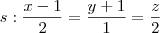
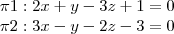
Sabendo que "r" e "s" são retas e ?1 e ?2 são planos, calcule a posição relativa entre:
a) (r, s)
b) (?1, ?2)
c) (s, ?1)
d) (r, ?2)
e) (s, ?2)
Na letra a e b, eu achei a resposta "reversas" e "concorrentes", respectivamente. Não sei se estão corretas, mas é um início, porque não conseguir nem começar as três últimas hehe.
-
jennakusterbeck
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 20, 2012 13:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Qui Set 20, 2012 15:45
por LuizAquino » Qui Set 20, 2012 15:45
jennakusterbeck escreveu:r: x = 2t
y = 1 - t
z = 2 + t
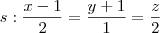
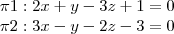
Sabendo que "r" e "s" são retas e ?1 e ?2 são planos, calcule a posição relativa entre:
a) (r, s)
b) (?1, ?2)
c) (s, ?1)
d) (r, ?2)
e) (s, ?2)
Na letra a e b, eu achei a resposta "reversas" e "concorrentes", respectivamente. Não sei se estão corretas, mas é um início, porque não conseguir nem começar as três últimas hehe.
Suas respostas estão corretas para os itens a) e b).
Para saber como resolver os outros itens, eu gostaria de recomendar a videoaula "17. Geometria Analítica - Posição Relativa Entre Reta e Plano". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoSe após assistir a videoaula você não conseguir terminar o exercício, então poste aqui até onde conseguiu avançar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jennakusterbeck » Qui Set 20, 2012 16:44
por jennakusterbeck » Qui Set 20, 2012 16:44
Olá, acabei de ver esse vídeo, foi bem útil, obrigada. Pelo que eu pude fazer/entender, deu que todas as retas eram concorrentes, oblíquas ao plano. Achei a resposta um pouco estranha, mas nenhum produto interno deu igual a zero, e os vetores não eram múltiplos =/ Está certo?
-
jennakusterbeck
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 20, 2012 13:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Qui Set 20, 2012 16:52
por LuizAquino » Qui Set 20, 2012 16:52
jennakusterbeck escreveu:Olá, acabei de ver esse vídeo, foi bem útil, obrigada.
Eu fico contente que tenha sido útil.
jennakusterbeck escreveu:Pelo que eu pude fazer/entender, deu que todas as retas eram concorrentes, oblíquas ao plano. Achei a resposta um pouco estranha, mas nenhum produto interno deu igual a zero, e os vetores não eram múltiplos =/ Está certo?
Sim, está certo.
Mas se o exercício tivesse pedido a posição relativa entre r e
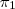
, note que a resposta seria: r é paralela a
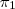
, sendo que r não está contida em
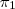
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jennakusterbeck » Qui Set 20, 2012 17:18
por jennakusterbeck » Qui Set 20, 2012 17:18
Obrigada

-
jennakusterbeck
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 20, 2012 13:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- posição relativa entre a reta r de equações paramétricas
por Ana Maria da Silva » Ter Jun 04, 2013 20:52
- 0 Respostas
- 1157 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 04, 2013 20:52
Geometria Analítica
-
- [Posição relativa de retas e planos - Geometria Analítica]
por Gustavo195 » Dom Abr 07, 2013 16:34
- 0 Respostas
- 2143 Exibições
- Última mensagem por Gustavo195

Dom Abr 07, 2013 16:34
Geometria Analítica
-
- posição relativa entre os planos
por Ana Maria da Silva » Ter Jun 04, 2013 10:38
- 2 Respostas
- 3012 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 04, 2013 20:31
Geometria Analítica
-
- posição relativa entre as retas r e pi
por Ana Maria da Silva » Qua Jun 05, 2013 11:55
- 0 Respostas
- 1127 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 05, 2013 11:55
Geometria Analítica
-
- [SUPERFICIE] Posição relativa de reta em uma sup esférica
por amigao » Sáb Jun 29, 2013 11:23
- 1 Respostas
- 1809 Exibições
- Última mensagem por young_jedi

Dom Jun 30, 2013 18:04
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
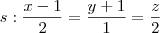
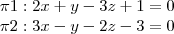



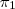 , note que a resposta seria: r é paralela a
, note que a resposta seria: r é paralela a 

 .
.



