OBS: Sistema de coordenadas adotado ortogonal.
Dados os planos
 ,
,  ,
,  , mostre que
, mostre que 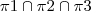 se reduz a um único ponto A (determine-o). Em seguida, calcule o volume do paralelepípedo que tem diagonal AH (H=(2,1,3)) e três faces contidas nos planos dados.
se reduz a um único ponto A (determine-o). Em seguida, calcule o volume do paralelepípedo que tem diagonal AH (H=(2,1,3)) e três faces contidas nos planos dados.Resposta;
V=65/3 u.v
Bom, o ponto A eu descobri fazendo um sistema com as equações gerais dos planos
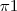 ,
, 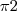 ,
,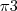 , agora o volume eu não consegui. Não consegui definir qual diagonal ele está se referindo. Em tempo, A=(1,1,-1).
, agora o volume eu não consegui. Não consegui definir qual diagonal ele está se referindo. Em tempo, A=(1,1,-1).Agradeço desde já.




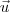 ,
,  e
e 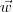 indicados na figura abaixo. A partir desse vetores, o volume do paralelepípedo será dado por
indicados na figura abaixo. A partir desse vetores, o volume do paralelepípedo será dado por 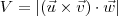 .
.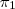 e
e 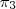 ;
;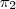 e
e 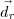 ,
, 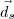 e
e 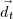 , respectivos a r, s e t nesta ordem.
, respectivos a r, s e t nesta ordem.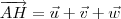 . Por outro lado, temos que existem escalares a, b e c tais que
. Por outro lado, temos que existem escalares a, b e c tais que 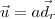 ,
, 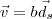 e
e 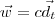 .
. ,
, 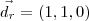
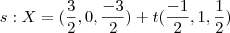 ,
, 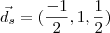
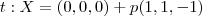 ,
, 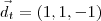
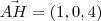
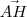 é combinação linear dos vetores
é combinação linear dos vetores 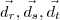 , vem:
, vem:
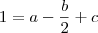

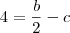
 ,
, 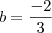 ,
, 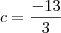
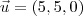
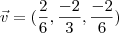
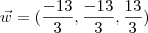
![[\vec{v},\vec{u},\vec{w}]=\frac{65}{3} [\vec{v},\vec{u},\vec{w}]=\frac{65}{3}](/latexrender/pictures/f3ae40407728e3528146bf61568a0790.png) , mas
, mas ![|[\vec{v},\vec{u},\vec{w}]|=V=\frac{65}{3} u.v |[\vec{v},\vec{u},\vec{w}]|=V=\frac{65}{3} u.v](/latexrender/pictures/dc5f6f4da8ab2c0138a6187faa36a174.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.