Leu escreveu:Obter a equação geral da superfície esférica tangente ao plano J: x+y-2=0 no ponto P=(0,2,0) e ao plano G: x+z+1. Encontre o ponto de tangência das superfícies com o plano G . Determine as coordenadas do centro e o raio do círculo que se obtém seccionando as superfícies de maior raio com o plano F:2X+Y-Z-7=0.
Oi galera, eu tentei fazer essa questão usando as fórmulas de distâcia, já que a superfície tangencia o plano, logo a distâcia do certro ao plano seria o raio, mas não
deu certo.Se alguém puder resolver essa questão para ver como é, ficarei muito agradecida.
Eu presumo que o plano G seja x + z + 1 = 0. Note que você esqueceu de digitar o " = 0".
Se C é o centro da esfera, então você já deve saber que PC é perpendicular ao plano J, já que P é o ponto de tangência.
Isso significa que C pertence a reta passando por P e que é perpendicular ao plano J. Nesse caso, um vetor diretor para essa reta coincide com o vetor normal desse plano. Sendo assim, as equações paramétricas dessa reta podem ser dadas por:
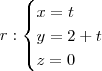
Como C pertence r, o formato do ponto C deve ser (t, 2 + t, 0), para algum escalar t.
Por outro lado, como a esfera é tangente a J e a G, devemos ter d(C, J) = d(C, G). Usando a fórmula para a distância entre ponto e plano, temos que:
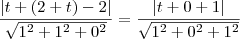
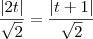
Agora tente continuar a partir daí. Basta resolver essa equação modular. Você irá obter dois valores possíveis para t. Sendo assim, há duas possibilidades para C. Isso significa que há duas esferas que atendem ao problema. Uma delas terá o raio maior do que a outra.


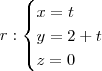
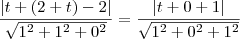
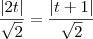



 , avisa que eu resolvo.
, avisa que eu resolvo.

