CarolMarques escreveu:A equação 7x²+24xy-256x-192y+1456=0 é uma hipérbole que por meio de rotação e translação eu cheguei numa equação reduzida x²/9-y²/16=1 o centro é C(8,6) e o angulo de rotação é o arc sen =3/5 (sen a =3/5 e cos a =4/5).
Ok. Mas é interessante você mudar as variáveis x e y conforme efetua as translações e rotações.
Por exemplo, ao realizar a translação você passou do sistema de eixos xOy para um outro sistema de eixos x'O'y'.
Em seguida, ao realizar a rotação você passou do sistema de eixos x'O'y' para um outro sistema de eixos uO''v.
Sendo assim, é interessante deixar a equação final com o formato:
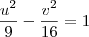
Isso ajuda a não fazer confusão sobre que sistema de eixos estamos no momento.
CarolMarques escreveu:Eu não sei achar as assintotas dessa hipérbole.
Se uma hipérbole é dada pela equação
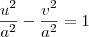
, então as assíntotas dessa hipérbole são
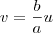
e
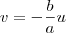
.
Portanto, as assíntotas da hipérbole
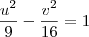
são dadas por
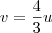
e
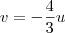
.
Precisamos agora aplicar uma rotação nessas assíntotas e depois uma translação. Desse modo, voltaremos para o sistema de eixos originais.
Para aplicar a rotação, basta realizar as substituições
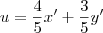
e
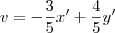
. Isso nos leva do sistema uOv para o sistema x'O'y'. Temos então que:
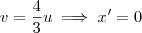
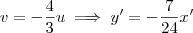
Agora para aplicar a translação, basta realizar as substituições
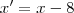
e
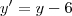
. Isso nos leva do sistema x'O'y' para o sistema xOy. Temos então que:

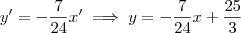
Portanto, as equações das assíntotas no sistema xOy são dadas por

e
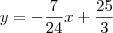
.



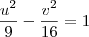
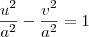 , então as assíntotas dessa hipérbole são
, então as assíntotas dessa hipérbole são 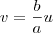 e
e 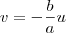 .
.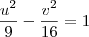 são dadas por
são dadas por 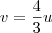 e
e 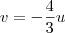 .
.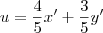 e
e 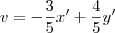 . Isso nos leva do sistema uOv para o sistema x'O'y'. Temos então que:
. Isso nos leva do sistema uOv para o sistema x'O'y'. Temos então que: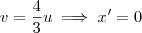
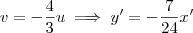
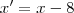 e
e 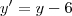 . Isso nos leva do sistema x'O'y' para o sistema xOy. Temos então que:
. Isso nos leva do sistema x'O'y' para o sistema xOy. Temos então que:
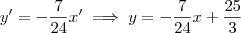
 e
e 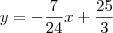 .
.





