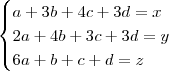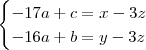elizabethec escreveu:Preciso determinar se v1=(1,2,6), v2=(3,4,1), v3=(4,3,1), v4=(3,3,1) geram R3.
Eu sei que para gerar o R3 os vetores presisam formar uma combinaçao linear, e com o determinante dos ceficientes eu consigo dizer se gera ou nao gera o R3, mas nesse exercicio acima nao consigo fazer por determinate como eu faço?
Seja um vetor
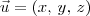
em
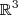
. Deseja-se verificar se existem escalares a, b, c e d tais que:
(x, y, z) = a(1, 2, 6) + b(3, 4, 1) + c(4, 3, 1) + d(3, 3, 1)
Ou seja, temos o sistema:
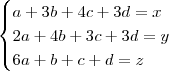
Esse sistema possui quatro incógnitas (a, b, c e d) e três equações. Ele pode ser impossível ou ele pode ser possível e indeterminado.
Vamos isolar a variável d na última equação e substituí-la nas outas duas. Ficamos apenas com:
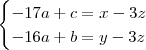
Temos então que:
b = y - 3z + 16a
c = x - 3z + 17a
d = 7z - x - y - 39a
Note que a incógnita
a é livre. Temos então infinitas soluções (ou seja, um sistema possível e indeterminado). Isso significa que existem escalares a, b, c e d que atendem a combinação linear.
Em particular, para a = 1, temos que:
b = y - 3z + 16
c = x - 3z + 17
d = 7z - x - y - 39
Sendo assim, podemos dizer que:
(x, y, z) = 1(1, 2, 6) + (y - 3z + 16)(3, 4, 1) + (x - 3z + 17)(4, 3, 1) + (7z - x - y - 39)(3, 3, 1)
Temos então que {(1, 2, 6), (3, 4, 1), (4, 3, 1), (3, 3, 1)} é um gerador de
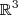
.


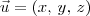 em
em 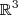 . Deseja-se verificar se existem escalares a, b, c e d tais que:
. Deseja-se verificar se existem escalares a, b, c e d tais que: