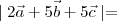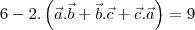por stuart clark » Seg Abr 09, 2012 12:16
por stuart clark » Seg Abr 09, 2012 12:16
If
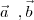
and
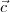
are three vectors such that
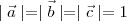
and

then
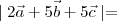
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Seg Abr 09, 2012 12:19
por stuart clark » Seg Abr 09, 2012 12:19
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Qua Abr 11, 2012 23:44
por stuart clark » Qua Abr 11, 2012 23:44
Thanks Moderator Got it

So

So

-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 11:13
por LuizAquino » Qui Abr 12, 2012 11:13
stuart clark escreveu:Thanks Moderator Got it

So

So

Ok.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
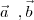 and
and 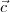 are three vectors such that
are three vectors such that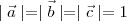 and
and 
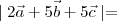

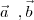 and
and 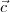 are three vectors such that
are three vectors such that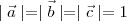 and
and