 por Clovis Eduardo » Dom Dez 11, 2011 18:12
por Clovis Eduardo » Dom Dez 11, 2011 18:12
Se A, B, C são vértices de um triângulo equilátero de lado unitário, calcule:
AB.BC + BC.CA + CA.AB
Bom a questao é essa... fiz o produto escalar entre os vertices...
e ficou uma resposta enorme..
provavelmente deve estar errada.
Obrigado
-
Clovis Eduardo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 09, 2011 02:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Seg Dez 12, 2011 18:02
por LuizAquino » Seg Dez 12, 2011 18:02
Clovis Eduardo escreveu:Se A, B, C são vértices de um triângulo equilátero de lado unitário, calcule:
AB.BC + BC.CA + CA.AB
Vide a figura abaixo.
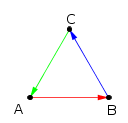
- figura.png (3.29 KiB) Exibido 2570 vezes
Note que:
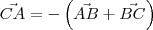
Sendo assim, temos que:
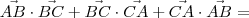
![\vec{AB}\cdot \vec{BC} + \vec{BC}\cdot \left[-\left(\vec{AB}+\vec{BC}\right)\right] + \left[-\left(\vec{AB}+\vec{BC}\right)\right]\cdot \vec{AB} \vec{AB}\cdot \vec{BC} + \vec{BC}\cdot \left[-\left(\vec{AB}+\vec{BC}\right)\right] + \left[-\left(\vec{AB}+\vec{BC}\right)\right]\cdot \vec{AB}](/latexrender/pictures/fab52098be487cc498fc1ee053900a9c.png)
Agora tente terminar o exercício.
DicasLembre-se das propriedades:
(i)

;
(ii)

;
(iii)
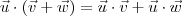
;
(iv)

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7373 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2996 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5216 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3409 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2387 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



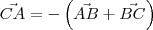
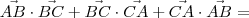
![\vec{AB}\cdot \vec{BC} + \vec{BC}\cdot \left[-\left(\vec{AB}+\vec{BC}\right)\right] + \left[-\left(\vec{AB}+\vec{BC}\right)\right]\cdot \vec{AB} \vec{AB}\cdot \vec{BC} + \vec{BC}\cdot \left[-\left(\vec{AB}+\vec{BC}\right)\right] + \left[-\left(\vec{AB}+\vec{BC}\right)\right]\cdot \vec{AB}](/latexrender/pictures/fab52098be487cc498fc1ee053900a9c.png)
 ;
; ;
;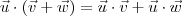 ;
; .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)