guileborges escreveu:Considere os subespa¸cos de R4,
W1 = [(1,?1, 0, 0), (0, 0, 1, 1)] e W2 = [(?2, 2, 1, 1), (1, 0, 0, 0)].
Seja W = W1 +W2.
guileborges escreveu:a) O vetor (2,?3, 2, 2) 2 W? Justifique.
Eu presumo que o texto seja na verdade "
O vetor (2,?3, 2, 2) pertence a W?".
O que você precisa analisar para responder essa pergunta é se esse vetor pode ser escrito como uma soma de dois vetores

e

de tal modo que
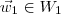
e
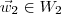
.
Ou seja, você precisa determinar se é possível escrever que
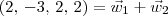
, com
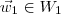
e
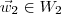
.
guileborges escreveu:b) Exiba uma base para W. Qual é a dimensão?
Você já sabe que o conjunto de vetores {(1,?1, 0, 0), (0, 0, 1, 1), (?2, 2, 1, 1), (1, 0, 0, 0)} gera W. Agora analise se esse conjunto de vetores é L.I.. Em caso positivo, então esse conjunto é uma base de W. Caso contrário, a partir desse conjunto, retirando algum vetor, você pode construir uma base de W.
A dimensão é simplesmente a quantidade de vetores na base.
guileborges escreveu:c) W1 �W2 = R4? Por quˆe?
Eu presumo que o texto seja na verdade "
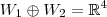 ? Por quê?
? Por quê?".
Para responder essa pergunta, você precisa analisar duas condições:
(i)
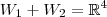
;
(ii)
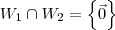
.
Se (i) e (ii) forem verdadeiras, então a reposta é sim. Caso contrário, a reposta é não.


 e
e  de tal modo que
de tal modo que 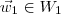 e
e 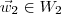 .
.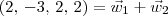 , com
, com 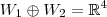 ? Por quê?
? Por quê?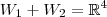 ;
;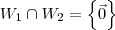 .
.