 por luiz_henriquear » Ter Out 25, 2011 20:07
por luiz_henriquear » Ter Out 25, 2011 20:07
Foi pedido a mim que determinasse o valor do módulo de

do versor v sendo que u=4i-5j+3k sendo qe i, j e k são vetores. Qual é a interpretação?
o resultado para o módulo seria
![\sqrt[2]{50} \sqrt[2]{50}](/latexrender/pictures/8763f5f1fc6a0f200886280c12e5389f.png)
e para o versor
![\frac{\sqrt[2]{50}}{25} \frac{\sqrt[2]{50}}{25}](/latexrender/pictures/36e04a926de618b81331839c4e563fc7.png)
?
-
luiz_henriquear
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Out 24, 2011 20:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia civil
- Andamento: cursando
 por MarceloFantini » Qua Out 26, 2011 15:14
por MarceloFantini » Qua Out 26, 2011 15:14
Um
versor é um vetor cujo módulo é igual a um. O
módulo de um vetor (ou
norma) é o comprimento do segmento formado pelos pontos, e é dado por:
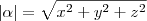
onde
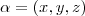
, por exemplo. Para encontrar o versor em relação a um vetor, basta pegar o vetor original e dividir cada coordenada pelo módulo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicio vetor e geometria analitica
por alexiakarina_ » Qui Mar 02, 2017 23:59
- 3 Respostas
- 5498 Exibições
- Última mensagem por alexiakarina_

Sáb Mar 04, 2017 17:28
Geometria Analítica
-
- Geometria Analitica ( Vetor)
por raf » Qui Jun 11, 2015 03:46
- 1 Respostas
- 7724 Exibições
- Última mensagem por nakagumahissao

Sex Jun 12, 2015 15:37
Geometria Analítica
-
- Geometria Analitica Vetor Unitario
por Diego Silva » Sáb Jul 20, 2013 12:14
- 6 Respostas
- 8834 Exibições
- Última mensagem por Diego Silva

Ter Jul 23, 2013 18:11
Geometria Analítica
-
- [Vetor Unitario] questao de geometria analítica 1
por spektroos » Seg Set 24, 2012 01:41
- 2 Respostas
- 4385 Exibições
- Última mensagem por spektroos

Seg Set 24, 2012 16:52
Geometria Analítica
-
- Geometria analítica : Vetor unitário ortogonal
por isabellasimao » Sáb Abr 11, 2020 15:37
- 2 Respostas
- 5337 Exibições
- Última mensagem por isabellasimao

Qua Abr 15, 2020 15:14
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 do versor v sendo que u=4i-5j+3k sendo qe i, j e k são vetores. Qual é a interpretação?
do versor v sendo que u=4i-5j+3k sendo qe i, j e k são vetores. Qual é a interpretação?![\sqrt[2]{50} \sqrt[2]{50}](/latexrender/pictures/8763f5f1fc6a0f200886280c12e5389f.png) e para o versor
e para o versor![\frac{\sqrt[2]{50}}{25} \frac{\sqrt[2]{50}}{25}](/latexrender/pictures/36e04a926de618b81331839c4e563fc7.png) ?
?
 do versor v sendo que u=4i-5j+3k sendo qe i, j e k são vetores. Qual é a interpretação?
do versor v sendo que u=4i-5j+3k sendo qe i, j e k são vetores. Qual é a interpretação?![\sqrt[2]{50} \sqrt[2]{50}](/latexrender/pictures/8763f5f1fc6a0f200886280c12e5389f.png) e para o versor
e para o versor![\frac{\sqrt[2]{50}}{25} \frac{\sqrt[2]{50}}{25}](/latexrender/pictures/36e04a926de618b81331839c4e563fc7.png) ?
?
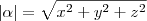
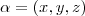 , por exemplo. Para encontrar o versor em relação a um vetor, basta pegar o vetor original e dividir cada coordenada pelo módulo.
, por exemplo. Para encontrar o versor em relação a um vetor, basta pegar o vetor original e dividir cada coordenada pelo módulo.
