a questão é essa
Seja o triângulo de vértices A(-1,4,2) B(3,-3,6) eC(2,-1,4) Escreva as equações paramétricas da reta que passa pelo ponto médio do lado AB e pelo vertice oposto C.
Bem, eu fiz desse seguinte jeito:
Pm=
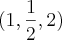 ==> ponto médio entre A e B
==> ponto médio entre A e B depois fiz
r= Pm+t(C-Pm) =
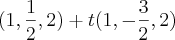
dessa forma a equação paramétrica da reta fica =>
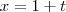
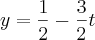
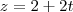
Só que a resposta no gabarito está diferente, está dessa forma:
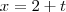
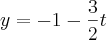
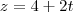
Pois bem... Estou desconfiando desse gabarito, pois algumas questões que resolvi deu alguns sinais trocados, uns valores diferentes. Então queria ver se a forma que fiz está realmente e se não tiver, apontar o erro.
Valeu



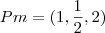 ==> ponto médio entre A e B
==> ponto médio entre A e B 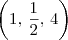 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

