-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480264 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539889 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503767 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 728510 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2165377 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por cal12 » Qua Set 14, 2011 11:05
por cal12 » Qua Set 14, 2011 11:05
Estou com um exercicio de vetor força que está respondido em forma de grafico e gostaria de saber como respondelo na forma analiteca por decomposiçao
EXECICIOO anel mostrado na figura 2.13a está submetido a duas forças F1 e F2. Se for necessario que a força resultante tenha intencidade de 1kn e seja orientada venticalmente para baixo, determine (a) a intencidade de F1 e F2, desde que

, (b) as intencidades de F1 e F2, se F2 for minima.
SOLUÇÃO
Parte (a). O desenpemho esquematico da adição dos vetores, de acordo com a lei do pararalelogramo, é mostrado na figura 2.13b pelo triangulo de vetores construidos na figura 2.13c, as intencidades desconhecidas F1 e F2 sao daterminadas usando-se a lei dos senos.
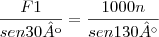

RESPOSTA
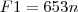
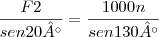

Parte (b). Se

não for especificado, entã, pelo triangulo de vetores (figura 2.13d), F2 pode ser adicionado a F1, de varias maneras para dar força resultante de 1000n. O comprimento ou intencidade minima de F2 ocorrera quando sua linha de ação for perpendicular a Fi qualquer outra direção, tal como OA ou OB, da um valor maior para F2, portanto quando
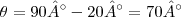
, F2 é minima pelo triangulo mostrado na figura 2.13e, ve-se que:
RESPOSTA
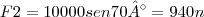


-
cal12
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Ago 14, 2011 11:21
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda em Vetor
por cal12 » Dom Ago 14, 2011 11:44
- 1 Respostas
- 955 Exibições
- Última mensagem por LuizAquino

Dom Ago 14, 2011 12:47
Geometria Analítica
-
- [Vetor definido por dois pontos] Ajuda!
por spektroos » Qui Set 27, 2012 17:04
- 1 Respostas
- 1499 Exibições
- Última mensagem por Russman

Qui Set 27, 2012 18:41
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4229 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 1734 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 7823 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 18 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , (b) as intencidades de F1 e F2, se F2 for minima.
, (b) as intencidades de F1 e F2, se F2 for minima. 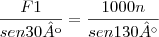

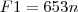
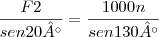

 não for especificado, entã, pelo triangulo de vetores (figura 2.13d), F2 pode ser adicionado a F1, de varias maneras para dar força resultante de 1000n. O comprimento ou intencidade minima de F2 ocorrera quando sua linha de ação for perpendicular a Fi qualquer outra direção, tal como OA ou OB, da um valor maior para F2, portanto quando
não for especificado, entã, pelo triangulo de vetores (figura 2.13d), F2 pode ser adicionado a F1, de varias maneras para dar força resultante de 1000n. O comprimento ou intencidade minima de F2 ocorrera quando sua linha de ação for perpendicular a Fi qualquer outra direção, tal como OA ou OB, da um valor maior para F2, portanto quando 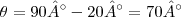 , F2 é minima pelo triangulo mostrado na figura 2.13e, ve-se que:
, F2 é minima pelo triangulo mostrado na figura 2.13e, ve-se que: