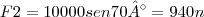EXECICIO
O anel mostrado na figura 2.13a está submetido a duas forças F1 e F2. Se for necessario que a força resultante tenha intencidade de 1kn e seja orientada venticalmente para baixo, determine (a) a intencidade de F1 e F2, desde que
 , (b) as intencidades de F1 e F2, se F2 for minima.
, (b) as intencidades de F1 e F2, se F2 for minima. SOLUÇÃO
Parte (a). O desenpemho esquematico da adição dos vetores, de acordo com a lei do pararalelogramo, é mostrado na figura 2.13b pelo triangulo de vetores construidos na figura 2.13c, as intencidades desconhecidas F1 e F2 sao daterminadas usando-se a lei dos senos.
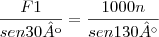

RESPOSTA
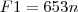
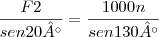

Parte (b). Se
 não for especificado, entã, pelo triangulo de vetores (figura 2.13d), F2 pode ser adicionado a F1, de varias maneras para dar força resultante de 1000n. O comprimento ou intencidade minima de F2 ocorrera quando sua linha de ação for perpendicular a Fi qualquer outra direção, tal como OA ou OB, da um valor maior para F2, portanto quando
não for especificado, entã, pelo triangulo de vetores (figura 2.13d), F2 pode ser adicionado a F1, de varias maneras para dar força resultante de 1000n. O comprimento ou intencidade minima de F2 ocorrera quando sua linha de ação for perpendicular a Fi qualquer outra direção, tal como OA ou OB, da um valor maior para F2, portanto quando 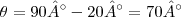 , F2 é minima pelo triangulo mostrado na figura 2.13e, ve-se que:
, F2 é minima pelo triangulo mostrado na figura 2.13e, ve-se que:RESPOSTA