 por -civil- » Ter Ago 09, 2011 21:49
por -civil- » Ter Ago 09, 2011 21:49
Boulos - 3ª ed. - Cap. 18
18-5) Obtenha, em cada caso, uma equação vetorial da reta que contém P, é paralela ou contida no plano  e é concorrente com a reta r.
e é concorrente com a reta r.
b) P = (1,0,1);  : x - 3y - z = 1; r: X = (0,0,0) +
: x - 3y - z = 1; r: X = (0,0,0) +  (2,1,-1)
(2,1,-1)
Verifiquei que P não pertece a

e que r é paralelo a

. E agora, como encontrar o plano formado entre P e r?
d) P = (2,-1,2);

: x + y +z = 0; r é a intersecção dos planos

1: x=z e

2: z = y + 2
Verifiquei que P não pertence a

e também não pertence a r. Mas como prosseguir?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Ago 11, 2011 23:31
por LuizAquino » Qui Ago 11, 2011 23:31
-civil- escreveu:Boulos - 3ª ed. - Cap. 18
18-5) Obtenha, em cada caso, uma equação vetorial da reta que contém P, é paralela ou contida no plano

e é concorrente com a reta r.
b) P = (1,0,1);

: x - 3y - z = 1; r: X = (0,0,0) +

(2,1,-1)
Verifiquei que P não pertece a

e que r é paralelo a

. E agora, como encontrar o plano formado entre P e r?
No próprio livro citado, há a seguinte proposição:
r e s são concorrentes se e somente se são coplanares e não são paralelas. Ou seja, se e somente se:

,
e

é L. I., sendo que

vetor diretor de r,

vetor diretor de s,

um ponto de r e

um ponto de s.
Note que pelos dados do exercício você pode obter o vetor
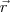
, um ponto A de r e um ponto B de s. Fica faltando

.
Além disso, perceba que como r e s são concorrentes e paralelas ao plano

, podemos tomar

de tal modo que

, sendo
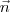
o vetor normal de

.
Unindo essa última informação com o determinante acima, você monta um sistema linear com três incógnitas (m, n e p) e duas equações. A partir disso você obtém

.
-civil- escreveu:d) P = (2,-1,2);

: x + y +z = 0; r é a intersecção dos planos
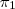
: x=z e
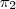
: z = y + 2
Verifiquei que P não pertence a

e também não pertence a r. Mas como prosseguir?
Note que r é perpendicular ao plano

. Para s ser paralela a

e concorrente a r, deve existir um ponto Q de r tal que

e

. Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Encontrar a eq. vetorial da reta
 por -civil- » Qua Ago 10, 2011 16:16
por -civil- » Qua Ago 10, 2011 16:16
- 3 Respostas
- 2444 Exibições
- Última mensagem por LuizAquino

Qui Ago 18, 2011 10:15
Geometria Analítica
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2418 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [Geometria Analítica] - Encontrar o módulo de s.
por Nicolas1Lane » Dom Mar 23, 2014 00:33
- 2 Respostas
- 1693 Exibições
- Última mensagem por Nicolas1Lane

Dom Mar 23, 2014 19:13
Geometria Analítica
-
- [Geometria Analítica] Encontrar os vértices do hexágono
 por -civil- » Qua Ago 10, 2011 16:51
por -civil- » Qua Ago 10, 2011 16:51
- 1 Respostas
- 2088 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 12:44
Geometria Analítica
-
- [reta] geometria analítica
 por Leidiana Catum » Seg Jul 14, 2008 00:06
por Leidiana Catum » Seg Jul 14, 2008 00:06
- 1 Respostas
- 11920 Exibições
- Última mensagem por admin

Seg Jul 14, 2008 02:34
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e é concorrente com a reta r.
e é concorrente com a reta r. : x - 3y - z = 1; r: X = (0,0,0) +
: x - 3y - z = 1; r: X = (0,0,0) +  (2,1,-1)
(2,1,-1) e que r é paralelo a
e que r é paralelo a  . E agora, como encontrar o plano formado entre P e r?
. E agora, como encontrar o plano formado entre P e r? : x + y +z = 0; r é a intersecção dos planos
: x + y +z = 0; r é a intersecção dos planos  1: x=z e
1: x=z e  2: z = y + 2
2: z = y + 2 e também não pertence a r. Mas como prosseguir?
e também não pertence a r. Mas como prosseguir?

 ,
,  é L. I., sendo que
é L. I., sendo que  vetor diretor de r,
vetor diretor de r,  vetor diretor de s,
vetor diretor de s,  um ponto de r e
um ponto de r e  um ponto de s.
um ponto de s.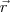 , um ponto A de r e um ponto B de s. Fica faltando
, um ponto A de r e um ponto B de s. Fica faltando  de tal modo que
de tal modo que  , sendo
, sendo 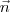 o vetor normal de
o vetor normal de 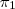 : x=z e
: x=z e 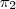 : z = y + 2
: z = y + 2 e
e  . Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo
. Após determinar esse ponto Q, basta tomar o vetor diretor de s como sendo  .
.