 por Civil UFSCar » Qua Jun 29, 2011 22:40
por Civil UFSCar » Qua Jun 29, 2011 22:40
Os focos desta hipérbole são (-5,0)(5,0), com amplitude focal 9/2
Já tentei de tudo, aprendi até como deduzir a amplitude focal de tanto tentar, mas achar a equação reduzida desta hipérbole eu não consigo...
usei 2b²/a=amplitude focal, substitui o ponto (5,9/4) na equação x²/a² - y²/b² = 1, mas só chego a valores errados...
A resposta certa é: x²/16 - y²/9 = 1
-
Civil UFSCar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 20, 2011 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Qui Jun 30, 2011 13:12
por LuizAquino » Qui Jun 30, 2011 13:12
Dica
Lembre-se que a distância entre os focos da hipérbole é 2c. Além disso, que c² = a² + b².
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Civil UFSCar » Qui Jun 30, 2011 23:15
por Civil UFSCar » Qui Jun 30, 2011 23:15
não me ajudou em nada, o "c" eu sei que é 5 já e que c²=a²+b²
-
Civil UFSCar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 20, 2011 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Jul 05, 2011 23:23
por LuizAquino » Ter Jul 05, 2011 23:23
Civil UFSCar escreveu:não me ajudou em nada, o "c" eu sei que é 5 já e que c²=a²+b²
Então você não está sabendo usar a dica.
Note que usando essas informações e os dados do exercício, você obtém o sistema:
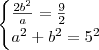
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por GiovanaBS » Dom Jul 26, 2015 17:47
por GiovanaBS » Dom Jul 26, 2015 17:47
Sabendo que os focos são (-5,0) e (5,0) temos c=5 e focos em Ox.
A amplitude focal é 9/2, logo b²=9.
a²=b²+c².
a²=-9+25, já que o b é sempre negativo.
a²=16, então:
x²/16 - y²/9=1
-
GiovanaBS
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jul 26, 2015 17:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Nao consigo achar a forma reduzida da matriz..
por PeIdInHu » Seg Jun 14, 2010 23:07
- 1 Respostas
- 2578 Exibições
- Última mensagem por PeIdInHu

Seg Jun 14, 2010 23:55
Matrizes e Determinantes
-
- equação reduzida
por Synval » Seg Abr 12, 2010 23:42
- 1 Respostas
- 1392 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:59
Sistemas de Equações
-
- Equação reduzida da reta
por Synval » Seg Abr 12, 2010 23:45
- 1 Respostas
- 1992 Exibições
- Última mensagem por Synval

Ter Abr 13, 2010 08:53
Cálculo: Limites, Derivadas e Integrais
-
- Equacao reduzida elipse
por Livingstone » Qua Jan 14, 2015 19:39
- 0 Respostas
- 1009 Exibições
- Última mensagem por Livingstone

Qua Jan 14, 2015 19:39
Geometria Analítica
-
- Equacao reduzida elipse
por Livingstone » Qua Jan 14, 2015 19:40
- 0 Respostas
- 1337 Exibições
- Última mensagem por Livingstone

Qua Jan 14, 2015 19:40
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.