 por valeuleo » Ter Mai 10, 2011 12:20
por valeuleo » Ter Mai 10, 2011 12:20
Estou resolvendo uma lista de geometria analítica e me deparei com uma questão onde o resultado que obtenho nuca é igual ao da apostila. A questão é:
Determine a distância do ponto D(2,3,3) ao plano determinado pelos pontos A(3,3,1), B(1,1,-3) e C(-1,3,0).
Eu obtenho a resposta
![\frac{25 \sqrt[]{174}}{174} \frac{25 \sqrt[]{174}}{174}](/latexrender/pictures/acc5e184a9d3b799b8d431edecad1a15.png)
. Mas a correta é
![\frac{5\sqrt[]{174}}{58} \frac{5\sqrt[]{174}}{58}](/latexrender/pictures/05511cc5548d6c285b235604db62e04b.png)
Me ajudem é urgente. Fiz todos os cálculos através da fórmula D =
![\frac{\left|ax+by+cz+d \right|}{\left|\sqrt[]{{a}^{2}+{b}^{2}+{c}^{2}} \right|} \frac{\left|ax+by+cz+d \right|}{\left|\sqrt[]{{a}^{2}+{b}^{2}+{c}^{2}} \right|}](/latexrender/pictures/ac09c83605b2be882fa83094bddd600a.png)
Escolhi os valores do ponto A para representarem x, y e z.
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por LuizAquino » Qua Mai 11, 2011 10:30
por LuizAquino » Qua Mai 11, 2011 10:30
O plano deve conter os pontos:
A = (3, 3, 1)
B = (1, 1, -3)
C = (-1, 3, 0)
Temos que:
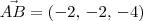
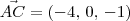
O vetor normal a esse plano será:
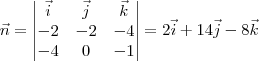
O plano contém, por exemplo, o ponto A. Sendo assim, temos que:
2(x - 3) + 14(y - 3) - 8(z - 1) = 0
x + 7y - 4z - 20 = 0
A distância entre o ponto D = (2, 3, 3) e esse plano será:
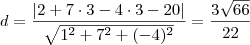
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Distancia entre ponto e plano
por teneral » Seg Jul 09, 2018 11:29
- 0 Respostas
- 5370 Exibições
- Última mensagem por teneral

Seg Jul 09, 2018 11:29
Geometria Analítica
-
- [Cálculo de distancia] Calcular a distancia de um ponto (B)
por girli » Dom Mai 18, 2014 17:59
- 1 Respostas
- 3894 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:43
Geometria Plana
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14964 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- distância do ponto
por leticiapires52 » Qua Set 24, 2014 13:02
- 1 Respostas
- 1050 Exibições
- Última mensagem por nakagumahissao

Qui Set 25, 2014 12:23
Geometria Analítica
-
- Distância de ponto à reta
por Jonatan » Qua Jul 07, 2010 11:24
- 1 Respostas
- 2734 Exibições
- Última mensagem por Tom

Qua Jul 07, 2010 13:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{25 \sqrt[]{174}}{174} \frac{25 \sqrt[]{174}}{174}](/latexrender/pictures/acc5e184a9d3b799b8d431edecad1a15.png) . Mas a correta é
. Mas a correta é ![\frac{5\sqrt[]{174}}{58} \frac{5\sqrt[]{174}}{58}](/latexrender/pictures/05511cc5548d6c285b235604db62e04b.png)
![\frac{\left|ax+by+cz+d \right|}{\left|\sqrt[]{{a}^{2}+{b}^{2}+{c}^{2}} \right|} \frac{\left|ax+by+cz+d \right|}{\left|\sqrt[]{{a}^{2}+{b}^{2}+{c}^{2}} \right|}](/latexrender/pictures/ac09c83605b2be882fa83094bddd600a.png)


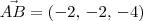
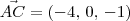
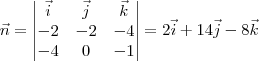
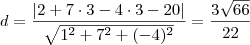

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
