-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480730 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542407 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506139 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 735284 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2181932 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Umumum » Seg Jun 30, 2008 20:32
por Umumum » Seg Jun 30, 2008 20:32
Sejam W1 e W2 subespaços de V de dimensão finita e suponha que

contém apenas o vetor nulo. Seja {e1, ..., em} uma base de W1, e {e'1, ..., e'n} uma base de W2. Mostre que {e1, ..., em, e'1, ..., e'n} é uma base do subespaço W = W1 + W2, onde W1 + W2 é conjunto de todos os vetores de V da forma x1 + x2, onde x1 pertence a W1 e x2 pertence a W2. Mostre ainda que dim(W) = dim(W1) + dim(W2)
não faço idéia para onde vai, alguém poderia ajudar-me?
-
Umumum
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 30, 2008 20:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia e Ciências dos Materiais
- Andamento: cursando
 por admin » Qui Jul 03, 2008 00:39
por admin » Qui Jul 03, 2008 00:39
Olá, boas-vindas!
Desculpe a demora em responder. Além de meu foco ser as dúvidas do Ensino Médio, nestes últimos dias tivemos um problema com um dos componentes do LaTeX no site, impossibilitando a exibição de novas fórmulas. E percebi justamente ao tentar enviar esta resposta ontem.
Como "estudante", adotaria a seguinte postura para entender como proceder na resolução, fica como sugestão:
-Em primeiro lugar, estude o que é um subespaço vetorial.
Há um tópico aqui com uma discussão relacionada, pode ajudar:
viewtopic.php?f=117&t=296#p757-Também estude o que é uma base vetorial.
Você verá que os vetores da base são linearmente independentes.
E que todos os vetores do subespaço considerado são gerados por estes vetores da base.
Por exemplo, como a base de
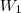
é

, a dimensão de
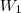
é

, e para cada vetor de
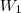
existe uma "m-upla" de escalares

tais que
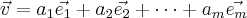
.
Quando eu escrevo para você "estudar o que é..." quero dizer para rever com atenção as definições e teoremas.
Em resumo, será necessário utilizar a existência destes escalares, juntamente com as condições de subespaço.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Umumum » Sex Jul 04, 2008 12:42
por Umumum » Sex Jul 04, 2008 12:42
Obrigado, finalmente uma luz nesse mar de escuridão.
O que vc sugeriu, foi exatamente o que fiz.
o que consegui encontrar, mas estou na dúvida se esse meu raciocínio é isso, pois para resolver, basei-me no link indicado e em um livro que tinha por aqui e gostaria de saber se posso considerar isso como certo:
Se x

W1, pode então ser escrito como :

--------(1)
E y

W2, então toma a forma:
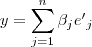
----------(2)
Se existir um z

W que seja z = x+y, onde z=
0, significa que y+x=
0, então
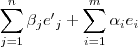
=
0 ------(3), isso significará que uma combinação linear dos vetores da base W1 e de W2 só resultará no vetor nulo se:

Em outras palavras, segnifica que {
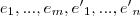
} é L.I.
Todo vetor de W é combinação linear de elementos de W1 e W2. Assim visto que z

W e z =
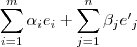
, logo:
a base de w é {

}
{
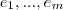
} é base de W1 --> Dim(W1) = m
{

} é base de W2 --> Dim(W2) = n
{
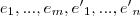
} é base de W --> Dim(W) = m + n => Dim(W) = Dim(W1)+Dim(W2)
-
Umumum
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 30, 2008 20:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia e Ciências dos Materiais
- Andamento: cursando
 por admin » Sex Jul 04, 2008 13:13
por admin » Sex Jul 04, 2008 13:13
Olá
Umumum, bom dia, fico feliz pela luz!
Acredito que sua resolução esteja correta sim, apenas um comentário.
Em todos os
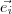
e
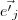
, faltou a notação de vetor.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Umumum » Sex Jul 04, 2008 14:04
por Umumum » Sex Jul 04, 2008 14:04
rapaz, se visse a dificuldade que tive para por essas formulas com esse editor daqui, vc n estaria estranhando a valta da notação do vetor
-
Umumum
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jun 30, 2008 20:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia e Ciências dos Materiais
- Andamento: cursando
 por admin » Sex Jul 04, 2008 15:05
por admin » Sex Jul 04, 2008 15:05
Olá.
Compreendo, mas aos poucos você se acostuma com a linguagem LaTeX.
O editor é apenas para facilitar, prevendo a expressão. Com o tempo, em geral, escrevemos diretamente.
Achei importante comentar porque apenas com símbolo

fica dito que
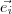
e
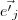
são, de fato, vetores.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 886
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Base de um espaco Vetorial!!!
por bigolasMan » Qui Mai 03, 2012 18:35
- 2 Respostas
- 1290 Exibições
- Última mensagem por bigolasMan

Qui Mai 03, 2012 22:44
Álgebra Linear
-
- Base do Espaço Vetorial
por biacrass » Sex Out 11, 2013 19:06
- 4 Respostas
- 2050 Exibições
- Última mensagem por Guilherme Pimentel

Qua Jan 15, 2014 06:03
Álgebra Linear
-
- Álgebra Linear Espaço Vetorial("base")
por Garota nerd » Seg Set 19, 2011 00:39
- 3 Respostas
- 2525 Exibições
- Última mensagem por LuizAquino

Seg Set 19, 2011 16:22
Álgebra Linear
-
- Problema de produto vetorial
por wizardie » Dom Abr 10, 2016 14:35
- 0 Respostas
- 860 Exibições
- Última mensagem por wizardie

Dom Abr 10, 2016 14:35
Álgebra Linear
-
- [Geometria Analítica]Problema de produto vetorial
por wizardie » Dom Abr 10, 2016 15:19
- 0 Respostas
- 1847 Exibições
- Última mensagem por wizardie

Dom Abr 10, 2016 15:19
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 contém apenas o vetor nulo. Seja {e1, ..., em} uma base de W1, e {e'1, ..., e'n} uma base de W2. Mostre que {e1, ..., em, e'1, ..., e'n} é uma base do subespaço W = W1 + W2, onde W1 + W2 é conjunto de todos os vetores de V da forma x1 + x2, onde x1 pertence a W1 e x2 pertence a W2. Mostre ainda que dim(W) = dim(W1) + dim(W2)
contém apenas o vetor nulo. Seja {e1, ..., em} uma base de W1, e {e'1, ..., e'n} uma base de W2. Mostre que {e1, ..., em, e'1, ..., e'n} é uma base do subespaço W = W1 + W2, onde W1 + W2 é conjunto de todos os vetores de V da forma x1 + x2, onde x1 pertence a W1 e x2 pertence a W2. Mostre ainda que dim(W) = dim(W1) + dim(W2)

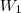 é
é  , a dimensão de
, a dimensão de  , e para cada vetor de
, e para cada vetor de  tais que
tais que 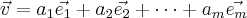 .
.
 W1, pode então ser escrito como :
W1, pode então ser escrito como : --------(1)
--------(1)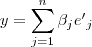 ----------(2)
----------(2)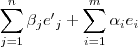 =
= 
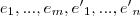 } é L.I.
} é L.I.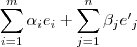 , logo:
, logo: }
}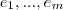 } é base de W1 --> Dim(W1) = m
} é base de W1 --> Dim(W1) = m } é base de W2 --> Dim(W2) = n
} é base de W2 --> Dim(W2) = n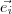 e
e 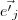 , faltou a notação de vetor.
, faltou a notação de vetor. fica dito que
fica dito que  } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: