Olá
leobcastro, boa tarde, seja bem-vindo!
Apenas completando sobre as condições para que
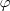
seja um subespaço vetorial, também deve ocorrer que o
elemento neutro do espaço vetorial
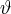
pertença a
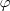
, ou seja:
iii)

Como um subespaço de um espaço vetorial é, ele mesmo, um espaço vetorial, em verdade, o subespaço deve satisfazer às 8 propriedades do espaço vetorial.
Mas, já sendo
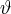
um espaço vetorial, estas 3 condições acima são suficientes para
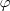
ser considerado um subespaço, pois as condições (i) e (ii) equivalem à verificação das duas primeiras de espaço vetorial, e a condição (iii) verifica as 6 demais.
Para você pensar um pouco mais sobre a "idéia" envolvida, considere o exemplo (a).
Veja que a equação

representa um plano:
Reflita sobre o que as propriedades (i), (ii) e (iii) "dizem":
(i) a soma de dois elementos do conjunto deve estar no conjunto!
(ii) um elemento do conjunto multiplicado um número real, também deve estar no conjunto!
(iii) o zero deve estar no conjunto!
A soma de dois elementos deste plano da figura, estará no plano?
Dado um elemento deste mesmo plano, multiplicado por um número real, ainda estará no plano?
E a origem, está no plano?
Esta é a idéia relacionada aos subespaços.
Veja a figura do outro exemplo (b), repare como a origem não está no conjunto:
Analise cada caso, cuidado pois nem sempre são planos, por exemplo o caso (e) onde há uma superfície parabólica ao longo do eixo x, sendo y sempre positivo, cuja visão planificada no plano xy é da função raiz quadrada:
Algebricamente, você pode fazer as provas que o Molina comentou.
Por exemplo, para o conjunto w do caso (a), considere dois pontos pertencentes a w:
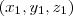
e
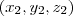
Como
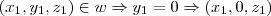
.
Analogamente,
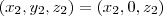
.
Fazendo a soma:
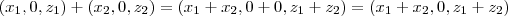
De modo que
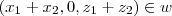
(pois a coordenada y é nula).
Fazendo o produto:
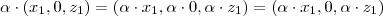
E também,
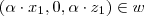
(pois a coordenada y é nula).
E é claro que
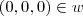
, como já comentado anteriormente.
Veja que foram verificadas as condições (i), (ii) e (iii), portanto o subconjunto
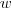
é um subespaço vetorial de
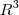
.
Em resumo, para as provas algébricas você pode fazer assim, considerando dois elementos do conjunto para a soma e verificando se a soma resultante está no mesmo "formato" da condição inicial. No exemplo (a) a condição inicial era apenas

, então, desde que o elemento resultante tenha a coordenada y nula, ele também pertence ao conjunto. Faça a mesma verificação após multiplicar um elemento por

.
Acredito que agora você consiga provar os outros casos. Segue como mais um exemplo a verificação de (e):
e)
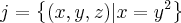
Sejam
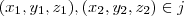
.
Então,

e

Somando os dois elementos:
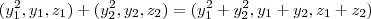
Como
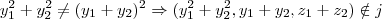
, logo, não vale a condição (i).
Já poderíamos parar por aqui, pois
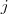
já não é um subespaço por não atender a uma das condições, mas vamos testar as outras...
Produto por um escalar:
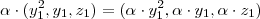
Como
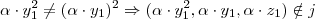
, portanto, não vale (ii).
Sobre o zero:
Partindo de
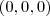
, verifica-se que:
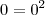
, ou seja, vale a condição (iii), de modo que
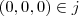
.
Note que apenas a condição (iii) foi verificada.
Espero ter ajudado!


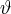 e
e 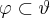 um subconjunto não vazio. Dizemos que
um subconjunto não vazio. Dizemos que 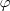 é um Subespaço Vetorial se são satisfeitas:
é um Subespaço Vetorial se são satisfeitas: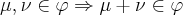
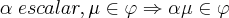


 representa um plano:
representa um plano: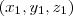 e
e 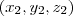
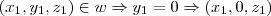 .
.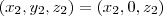 .
.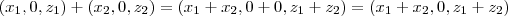
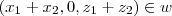 (pois a coordenada y é nula).
(pois a coordenada y é nula).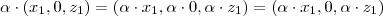
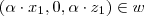 (pois a coordenada y é nula).
(pois a coordenada y é nula).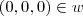 , como já comentado anteriormente.
, como já comentado anteriormente.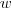 é um subespaço vetorial de
é um subespaço vetorial de 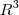 .
. .
.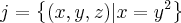
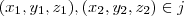 .
.

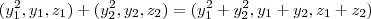
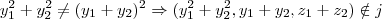 , logo, não vale a condição (i).
, logo, não vale a condição (i).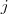 já não é um subespaço por não atender a uma das condições, mas vamos testar as outras...
já não é um subespaço por não atender a uma das condições, mas vamos testar as outras...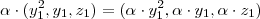
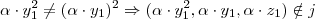 , portanto, não vale (ii).
, portanto, não vale (ii).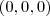 , verifica-se que:
, verifica-se que: 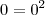 , ou seja, vale a condição (iii), de modo que
, ou seja, vale a condição (iii), de modo que 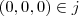 .
.
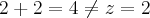
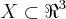 formado pelos vetores v=(x,y,z) tais que x.y = 0
formado pelos vetores v=(x,y,z) tais que x.y = 0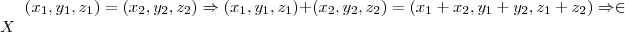

![{[algo]} = {x}\cdot{y} {[algo]} = {x}\cdot{y}](/latexrender/pictures/9d56567800fbc9f7f143a25bf58936be.png)