 por Raquel Botura » Sex Nov 09, 2018 11:19
por Raquel Botura » Sex Nov 09, 2018 11:19
[EQUAÇÃO VETORIAL E PARAMÉTRICA DA RETA NO PLANO]
Bom dia, gostaria de ajuda em Vetor diretor de uma reta NO PLANO e com a equação vetorial/paramétrica. Estou estudando para um exame de Portugal e neste caso, cobram essa matéria lá, e no Brasil, é encaixada no ensino superior.
A matéria em si eu entendi, porém to com dúvida nos exercícios cobrados e visto que quando busco vídeo aulas etc só encontro as equações usando o vetor no espaço (xo,yo,zo), enquanto nesse caso estão pedindo (xo,yo).
"A equação vetorial da reta que passa pelos pontos A(1,?5) e B(3,1) é
(x,y)=(?1/3,?m)+k(1/3,n)? k?R, em que:
ai é pedido o valor de m e n, sendo o gabarito m=9; n=1"
E outro bem similar mas ao invés de 2 pontos, é dado um ponto e o vetor diretor.
"Uma equação vetorial da reta que passa pelo ponto (?2,4) é paralela ao vetor (0,5) é
(x,y)=(a,?7)+k(b,2)?k?R, em que:
sendo O gabarito a=-2; b=0"
Nesses exercícios eu não entendo como achar esses valores, no primeiro exercício eu tentei substituir os valores na equação da reta que pode se achar utilizando os dois pontos dados, mas chutando, porque eu não acho que seja assim. Desculpa se estou pedindo muito, mas meu conhecimento sobre geometria analítica se limita a distância entre pontos, distância entre ponto e reta que é o que é cobrado aqui no Brasil. Se alguém puder me ajudar eu agradeço muito!
Obrigada, Raquel.
-
Raquel Botura
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Nov 09, 2018 10:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: cursinho para medicina em portugal
- Andamento: cursando
 por Gebe » Sex Nov 09, 2018 17:13
por Gebe » Sex Nov 09, 2018 17:13
Fiz o desenho abaixo para facilitar a explicação.
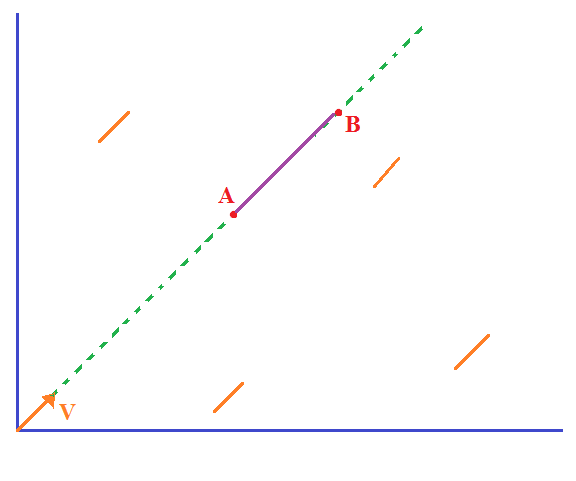
- vetores.png (8.11 KiB) Exibido 8383 vezes
No desenho temos o ponto A, o ponto B e o vetor diretor V.
Perceba que V em laranja é um vetor com mesma direção do segmento dado por AB (roxo), porém o modulo (tamanho) e a posição no plano cartesiano podem variar como sugere os vários vetores laranjas dispostos no desenho.
Assim sendo, a primeira coisa que devemos notar é que AB (roxo) tem a mesma direção que o vetor dado (1/3 , n). Não sabemos o tamanho desse vetor dado, mas sabemos que deve ser um pedacinho de AB ou um alongamento de AB.
Resumindo:
(1/3 , n) = t.(AB)
Onde "t" é um escalar (um numero como 0.8 ou 3, por exemplo).
Assim sendo podemos calcular "n".
AB = B - A = (3-1 , 1 + 5) = (2 , 6)
Substituindo:
(1/3 , n) = t. (2 , 6)
Montamos um sistema:
1/3 = 2t
n = 6t
Resolvendo teremos n = 3 * (1/3) = 1.
Agora para achar "m" podemos fazer de algumas formas diferentes, vou fazer da forma que acho mais simples.
Temos e equação vetorial (agora com n=1) dada por:
(x , y) = (?1/3 , ?m) + k.(1/3 , 1)
Sabemos que, na formulação da eq. vetorial, (-1/3 , -m) representa um ponto na reta.
Sabemos também que A e B são pontos da mesma reta, logo podemos substituir B (ou A) na equação da reta.
B = (-1/3 , -m) + k.(1/3 , 1)
(3 , 1) = (-1/3 , -m) + k.(1/3 , 1)
Montando um sistema:
3 = -1/3 + k.(1/3)
1 = -m + k
k = (3+1/3)/(1/3)
k = 10
1 = -m + 10
-m = -9
m = 9
2)
Semelhante ao primeiro.
V = (0 , 5)
V = t . (b , 2)
Montando o sistema:
0 = t.b
5 = 2t
t = 2.5 -> b = 0
Substituindo na eq. da reta o ponto dado e o valor de "b":
(-2 , 4) = (a , -7) + k.(0 , 2)
-2 = a + 0 . k
a = -2
Espero ter ajudado, qualquer duvida deixe msg.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5367 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2943 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Equação do plano
por manuoliveira » Qua Mai 23, 2012 17:59
- 1 Respostas
- 1968 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 20:48
Geometria Analítica
-
- Equação do plano
por Danilo » Qui Out 25, 2012 22:38
- 7 Respostas
- 7126 Exibições
- Última mensagem por MarceloFantini

Qua Out 31, 2012 06:51
Geometria Analítica
-
- {Equação do plano}
por Danilo » Sex Out 26, 2012 01:15
- 2 Respostas
- 2262 Exibições
- Última mensagem por Danilo

Sex Out 26, 2012 10:31
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


