 por pedrolinhares » Dom Jun 18, 2017 18:22
por pedrolinhares » Dom Jun 18, 2017 18:22
Boa tarde!
Estou há um tempo tentando resolver este exercício mas não consigo chegar em uma conclusão. Já tentei substituir z na equação do hiperbolóide, mas depois de desenvolver não consigo chegar á lugar nenhum. Se puderem ajudar, fico agradecido.
Exercício: Verificar que a interseção do plano
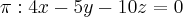
com o hiperbolóide de uma folha

consiste de duas retas e achar suas equações paramétricas.
Obrigado desde já.
-
pedrolinhares
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 18, 2017 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia eletronica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Interseção de dois planos
por bibs » Qui Ago 27, 2009 16:22
- 0 Respostas
- 5221 Exibições
- Última mensagem por bibs

Qui Ago 27, 2009 16:22
Geometria Analítica
-
- Interseção de dois planos
por bibs » Qui Ago 27, 2009 16:28
- 0 Respostas
- 2170 Exibições
- Última mensagem por bibs

Qui Ago 27, 2009 16:28
Geometria Analítica
-
- [Interseção entre planos]
por sulafuly » Dom Mar 02, 2014 01:14
- 0 Respostas
- 2016 Exibições
- Última mensagem por sulafuly

Dom Mar 02, 2014 01:14
Geometria Analítica
-
- Interseção entre planos
por marinasaboia » Sex Jan 08, 2016 14:44
- 1 Respostas
- 3229 Exibições
- Última mensagem por RuuKaasu

Sex Jan 15, 2016 21:52
Geometria Analítica
-
- Analítica - Interseção de retas e planos
por pedro_kampos » Qui Jul 24, 2014 23:49
- 1 Respostas
- 2429 Exibições
- Última mensagem por pedro_kampos

Dom Jul 27, 2014 20:59
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
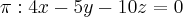 com o hiperbolóide de uma folha
com o hiperbolóide de uma folha  consiste de duas retas e achar suas equações paramétricas.
consiste de duas retas e achar suas equações paramétricas.

