 por EloiCamara » Ter Jan 10, 2017 12:44
por EloiCamara » Ter Jan 10, 2017 12:44
Alguém sabe como resolver essa questão?
"Determine o raio e as coordenadas do centro do círculo, que se obtém seccionando a superfície esférica S: x²+y²+z²=16 com o plano a:x+y+z-1= 0"
-
EloiCamara
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 10, 2017 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia da Computação
- Andamento: cursando
 por adauto martins » Qui Jan 12, 2017 14:46
por adauto martins » Qui Jan 12, 2017 14:46

a curva sera a intersecçao de

,ou seja
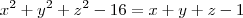
,agora um pouco de algebrismo para completar os quadrados,teremos:
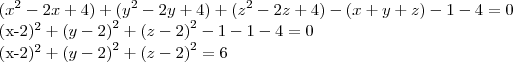
q. sera a equaçao da circunferencia no espaço de centro
![(2,2,2)...r=\sqrt[]{6}... (2,2,2)...r=\sqrt[]{6}...](/latexrender/pictures/5bc529ecc970dfdcdfced24c8a04ce65.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Superfície Esférica
por iarapassos » Ter Set 18, 2012 23:24
- 4 Respostas
- 4528 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:17
Geometria Analítica
-
- Superfície Esférica
por iarapassos » Sex Set 21, 2012 17:24
- 1 Respostas
- 1541 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:30
Geometria Analítica
-
- [SUPERFICIE] Esférica. num tetraedro
por amigao » Sáb Jun 29, 2013 22:39
- 1 Respostas
- 1576 Exibições
- Última mensagem por young_jedi

Dom Jun 30, 2013 14:34
Geometria Analítica
-
- [SUPERFICIE] Posição relativa de reta em uma sup esférica
por amigao » Sáb Jun 29, 2013 11:23
- 1 Respostas
- 2087 Exibições
- Última mensagem por young_jedi

Dom Jun 30, 2013 18:04
Geometria Analítica
-
- COORDENADAS ESFÉRICA
por ALEXSANDRO » Qua Jun 06, 2012 02:56
- 3 Respostas
- 2035 Exibições
- Última mensagem por LuizAquino

Qua Jun 06, 2012 19:44
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ,ou seja
,ou seja 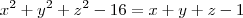 ,agora um pouco de algebrismo para completar os quadrados,teremos:
,agora um pouco de algebrismo para completar os quadrados,teremos: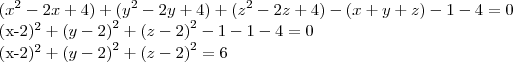
![(2,2,2)...r=\sqrt[]{6}... (2,2,2)...r=\sqrt[]{6}...](/latexrender/pictures/5bc529ecc970dfdcdfced24c8a04ce65.png)


 .
.
 :
: