 por Jamilly » Ter Mar 16, 2010 10:12
por Jamilly » Ter Mar 16, 2010 10:12
Bom dia!!

Estou estudando para um concurso e me deparei com uma questão que me deixou em dúvida! Espero que possam me ajudar!
A questão é a seguinte:
Resolva a seguinte inequação em R (reais) e responda na forma de intervalo:
1/x²-1 < 1/x³-1 (1 sobre x²-1 menor que 1 sobre x³-1)Minha resolução:
Eu passei a parte igualada para o lado esquerdo e ficou assim:
1/x²-1 - (1/x³-1) < 0Tirando o mmc:
x³-1 - (x²-1)/ (x²-1)(x³-1)< 0Simplificando:
x³-x² / (x²-1)(x³-1)< 0Decompus o denominador e o primeiro termo do numerador:
x²(x-1) / (x+1)(x-1)(x³-1)< 0Anulei (x-1) embaixo e em cima:
x² / (x+1)(x³-1)< 0Eu fiz o quadro de sinais e a resposta na forma de intervalo ficou:
[0,1]Mas acho que está errado, devo ter errado algo na resolução.
Peço que me ajudem.
-
Jamilly
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Mar 11, 2010 10:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por MarceloFantini » Ter Mar 16, 2010 22:57
por MarceloFantini » Ter Mar 16, 2010 22:57
Boa noite.
Vou multiplicar os dois lados por

:
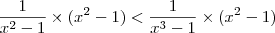
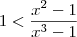
Multiplicando os dois lados por
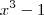
:
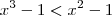

Agora pelo gráfico fica fácil perceber. Estou sem meios pra fazer um, mas se fizer perceberá que a condição é satisfeita apenas para
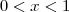
e
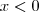
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Ter Mar 16, 2010 23:14
por Elcioschin » Ter Mar 16, 2010 23:14
Vou continuar e corrigir os cálculos de Jamilly:
1/(x² - 1) < 1/(x³ - 1)
1/(x² - 1) - 1/(x³ - 1) < 0 ----> Fatorando:
1/(x + 1)*(x - 1) - 1/(x - 1)*(x² + x + 1) < 0 ----> MMC = (x + 1)*(x - 1)*(x² + x + 1):
[(x² + x + 1) - (x + 1)]/ (x + 1)*(x - 1)*(x² + x + 1) < 0
x²/(x + 1)*(x - 1)*(x² + x + 1) < 0 ----> x² é sempre positivo e (x² + x + 1) também (concavidade p/cima e delta < 0)
Logo o sinal depende apenas de (x + 1)*(x - 1) ----> Parábola c/concavidade p/ cima ----> -1 < x < + 1
Temos, entretanto, uma restrição ----> X <> 0
Solução final: -1 < x < 0 e 0 < x < +1
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Ter Mar 16, 2010 23:29
por MarceloFantini » Ter Mar 16, 2010 23:29
Elcio, então qual seria o meu erro? E não entendi que a sua restrição. É

ou
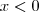
?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Qua Mar 17, 2010 13:26
por Elcioschin » Qua Mar 17, 2010 13:26
Fantini
a) O erro cometido foi multiplicar os dois membros por (x² - 1) devido ao seguinte:
1) Se (x² - 1) > 0 não há nenhum problema na multiplicação.
2) Se (x² - 1) < 0 ao se multiplicar o sinal da inequação deveria ter sido invertido.
Logo, esta multiplicação implica em resultados falsos.
b) x < > 0 significa "x diferente de zero".
Usei esta convenção para não ter o trabalho de escrever o símbolo de "diferente de" no LaTeX
Editado pela última vez por
Elcioschin em Qua Mar 17, 2010 20:52, em um total de 1 vez.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Jamilly » Qua Mar 17, 2010 20:24
por Jamilly » Qua Mar 17, 2010 20:24

Obrigada pela ajuda!
Vou tentar resolver e depois responda se tiver conseguido!!

-
Jamilly
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Mar 11, 2010 10:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6491 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda questão calculo
 por CarolAlves » Dom Out 04, 2015 20:28
por CarolAlves » Dom Out 04, 2015 20:28
- 2 Respostas
- 2732 Exibições
- Última mensagem por adauto martins

Qui Out 08, 2015 18:10
Cálculo: Limites, Derivadas e Integrais
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12993 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Ajuda de Calculo 2?
por edu2012 » Ter Mai 29, 2012 16:38
- 2 Respostas
- 6810 Exibições
- Última mensagem por edu2012

Qua Mai 30, 2012 09:24
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 2 AJUDA
por rodrigojuara » Seg Jun 15, 2015 23:38
- 0 Respostas
- 7442 Exibições
- Última mensagem por rodrigojuara

Seg Jun 15, 2015 23:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 :
: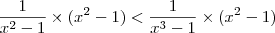
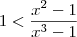
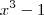 :
: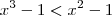

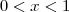 e
e 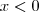



 ou
ou 


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.