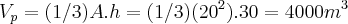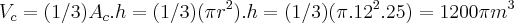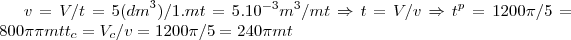por nda » Sex Dez 12, 2014 07:46
por nda » Sex Dez 12, 2014 07:46
Agradeço desde já!!!

A pirâmide de Quéfren, em Gizé, tem base quadrada cujo lado mede 214,5m e o volume mede aproximadamente 2199292 m³, calcule a altura dessa pirâmide(use valores aproximados.
Supondo que mudássemos a base da pirâmide, que é um quadrado de lado 1m, para um circulo de modo a manter a mesma altura de 4m e o mesmo volume. Qual deverá ser o raio desse círculo? (use ? = 3).
3)Calcule o volume de uma pirâmide de base hexagonal de lado 6m e altura 12m.
4) Sejam dois tanques ,um em forma de pirâmide de base quadrada de lado 20m e altura 30m , e um de formato de cone de raio 12m e altura 25m, sabendo disso responda:
a) Qual o volume dos dois tanques?
b) Supondo que se deseje encher esses tanques com água com uma vazão de 5 litros por minuto, em quanto tempo os dois tanques ficarão cheios? E qual tanque se encherá mais rápido?
-
nda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Dez 12, 2014 07:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por adauto martins » Sex Dez 12, 2014 11:28
por adauto martins » Sex Dez 12, 2014 11:28
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por nda » Sex Dez 12, 2014 13:32
por nda » Sex Dez 12, 2014 13:32
obg.. adauto martins..

-
nda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Dez 12, 2014 07:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me Ajude Por Favor Preciso disso ainda hoje!
 por masterdzs » Ter Mai 15, 2018 22:00
por masterdzs » Ter Mai 15, 2018 22:00
- 1 Respostas
- 6371 Exibições
- Última mensagem por Gebe

Ter Mai 15, 2018 23:48
Funções
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2606 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:47
Funções
-
- Preciso da Resolução desse exercicio
por alexcaju » Sex Jan 17, 2014 19:58
- 0 Respostas
- 1071 Exibições
- Última mensagem por alexcaju

Sex Jan 17, 2014 19:58
Matemática Financeira
-
- [Derivadas] Exercícios para estudar - ME AJUDEM POR FAVOR
 por Matheus_Silva » Sáb Jun 22, 2013 02:13
por Matheus_Silva » Sáb Jun 22, 2013 02:13
- 0 Respostas
- 2679 Exibições
- Última mensagem por Matheus_Silva

Sáb Jun 22, 2013 02:13
Cálculo: Limites, Derivadas e Integrais
-
- me ajudem por favorrrrrr!!!! trabalho d matematica!!!
por anaana363 » Ter Mai 11, 2010 22:11
- 1 Respostas
- 1416 Exibições
- Última mensagem por Molina

Ter Mai 11, 2010 22:43
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



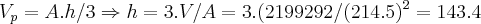
![{V}_{p}/{V}_{q}=(1/3)A.h/A'.h=(1/3)A/A'=(1/3).1/(\pi{r}^{2})=1\Rightarrow r=\sqrt[]{3.\pi} {V}_{p}/{V}_{q}=(1/3)A.h/A'.h=(1/3)A/A'=(1/3).1/(\pi{r}^{2})=1\Rightarrow r=\sqrt[]{3.\pi}](/latexrender/pictures/e22b48ea313a2e0a3d1217e11d730147.png)
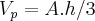 ,
,![A=6.{A}_{tr.equil}=6.(6.\sqrt[]{3}/4)=9\sqrt[]{3} A=6.{A}_{tr.equil}=6.(6.\sqrt[]{3}/4)=9\sqrt[]{3}](/latexrender/pictures/37dfba662f633b3a6e74202a14c8fe6d.png)
![\Rightarrow {V}_{p}=(9\sqrt[]{3}.12)/3=36\sqrt[]{3} \Rightarrow {V}_{p}=(9\sqrt[]{3}.12)/3=36\sqrt[]{3}](/latexrender/pictures/20f71cd56e5127b7313bd2880d926b1b.png)