O assunto é Vetores.
Quando trabalhamos com uma base ortonormal, sabe-se que pode ser positiva ou negativa. Contudo, explicaram-me que, no caso de ser positiva, significa que os três vetores tais que constituem a sequencia linearmente independente, base, estão ordenados de tal maneira que, sendo (u, v, p) uma,
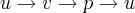. Agora, caso trata-se de uma base negativa, então 
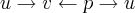, por exemplo, já nos informa que realmente é negativa, isto é, qualquer alteração na orientação, como na forma exemplificada, já é um sinal de base negativa. Por outro lado, estudando através de um livro, entendi que se temos, por exemplo, uma base negativa (a, b, c) então 
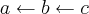e, dizemos que tal base é, na verdade, uma permutação não cíclica de (c, b, a), uma base positiva, 
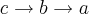. Contudo, estou confusa. A explicação do livro está mais claro, porém o professor não explicou dessa forma e, sim, da primeira. Tal explicação não estou conseguindo assimilar com a do livro. Por favor, gostaria de ajuda para esclarecer.... Obrigada ! Se puderem ser rápidos.... agradeço (a prova está chegando).
, avisa que eu resolvo.
