 por amigao » Sáb Jun 29, 2013 11:23
por amigao » Sáb Jun 29, 2013 11:23
Seja r X=(1,0,a) +

(a,a,0) e S:
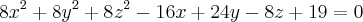
Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
Eu tentei fazer porém aparece o lambda no meio me atrapalhando e não consigo tirá-lo e nem continuar. Como faço?
grato.
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Dom Jun 30, 2013 18:04
por young_jedi » Dom Jun 30, 2013 18:04
reescrevendo a equação da esfera temos
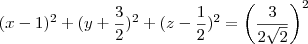
com isso temos o raio e o centro da esfera
agora si a reta é tangente a esfera então a distancia do centro ate a reta é igual ao raio. Então escolhemos um ponto qualquer da reta, por conveniência vamos escolher o ponto onde lambda é igual a zero ou seja o ponto
(1,0,a)
então fazendo o ponto central da esfera menos esse ponto teremos o vetor

calculando o modulo do produto vetorial deste vetor pelo vetor diretoo da reta e dividindo pelo modulo do vetor diretor teremos a distancia da reta ao cento que deve ser igual ao raio
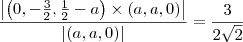
tente concluir, comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- posição relativa entre a reta r de equações paramétricas
por Ana Maria da Silva » Ter Jun 04, 2013 20:52
- 0 Respostas
- 1310 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 04, 2013 20:52
Geometria Analítica
-
- [Geometria Analítica] Posição relativa entre reta e plano
por jennakusterbeck » Qui Set 20, 2012 13:52
- 4 Respostas
- 3574 Exibições
- Última mensagem por jennakusterbeck

Qui Set 20, 2012 17:18
Geometria Analítica
-
- Superfície Esférica
por iarapassos » Ter Set 18, 2012 23:24
- 4 Respostas
- 4539 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:17
Geometria Analítica
-
- Superfície Esférica
por iarapassos » Sex Set 21, 2012 17:24
- 1 Respostas
- 1544 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:30
Geometria Analítica
-
- [Superficie Esférica]
por EloiCamara » Ter Jan 10, 2017 12:44
- 1 Respostas
- 1868 Exibições
- Última mensagem por adauto martins

Qui Jan 12, 2017 14:46
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (a,a,0) e S:
(a,a,0) e S: 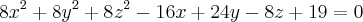 Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
 (a,a,0) e S:
(a,a,0) e S: 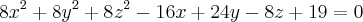 Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
Determine a para que (a) r seja tangente (b) secante (c) exterior a S.
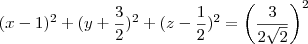

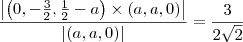


 .
.



