primeiro vamos encontrar a equação da reta AC
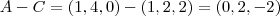
portanto a equação da reta sera
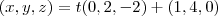

existe um ponto nesta reta que ligado ate o ponto B forma a reta da altura relativa com relação a B, então o vetor diretor desta reta terá que ser perpendicular a reta AC portanto o produto escalar do vetor direto de ambas as retas é igual a zero ou seja:
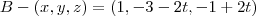

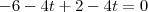

portanto o ponto onde a reta da altura relativa a B se encontra com a reta AC é

agora é so encontrar a reta que contem este ponto e o ponto B
comente as duvidas




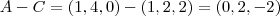
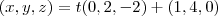

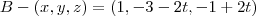

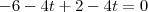



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)