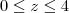Quádrica - identificar quádrica

[renan_a]

Fala pessoal , beleza.
Estou com um exercício do livro vetores e geometria analítica, do paulo winterle , e não consigo resolver o seguinte exercícios::

identificar e representar graficamente as superfífices expressas pelas equações nos intervalos dados:

m) y² - x² = 16 0z4

Meu professor geralmente pede que mostremos as 3 interseções, ou seja
quando z = 0 , tenho y² - x² = 16 = hipérbole equilátera
quando x=0 , tenho y² = 14 --> y= +/- 4
quando y=0 , tenho x² = -16 --> x= sem raiz real

Até aqui, é isso??

o segundo passo seria igualar a variável em que está servindo de eixo de rotação da superfície às delimitações do problema, ou seja, z=0 e z=4 , porém não consigo fazer isso, pois ela não está na equação...
Como devo proceder para encontrar o ponto, conica, etc que pode haver em z=0 e z=4 para eu poder desenhar a superfície

[LuizAquino]

identificar e representar graficamente as superfífices expressas pelas equações nos intervalos dados:

m) y² - x² = 16

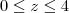
Meu professor geralmente pede que mostremos as 3 interseções, ou seja
quando z = 0 , tenho y² - x² = 16 = hipérbole equilátera
quando x=0 , tenho y² = 14 --> y= +/- 4
quando y=0 , tenho x² = -16 --> x= sem raiz real

Até aqui, é isso??

Você esqueceu de mencionar que quando x = 0 temos que y = 4 e y = -4 são retas paralelas ao eixo z (e passando, respectivamente, por (0, 4, 0) e (0, -4, 0)).

o segundo passo seria igualar a variável em que está servindo de eixo de rotação da superfície às delimitações do problema, ou seja, z=0 e z=4 , porém não consigo fazer isso, pois ela não está na equação...

Bem, o eixo z não está servindo como "eixo de rotação" nesse caso. Quando você fizer o esboço da superfície perceberá que ela não é formada através de uma revolução.

Como devo proceder para encontrar o ponto, conica, etc que pode haver em z=0 e z=4 para eu poder desenhar a superfície

Vamos pensar um pouco... "Traduzindo" o que o exercício diz, dado um ponto P = (x, y, z) dessa superfície, temos que para qualquer z no intervalo [0, 4] irá acontecer que y² - x² = 16.

Vamos escolher, por exemplo, z = 4. Geometricamente falando, o que significa z = 4? Ora, sabemos que isso representa um plano paralelo a xy e que passa por (0, 0, 4). Temos ainda que para os pontos P = (x, y, 4) da superfície, devemos ter y² - x² = 16. Juntando essas informações, temos que sobre o plano z = 4 a superfície formará a hipérbole y² - x² = 16.

Generalizando a ideia, temos que para z = k, com k no intervalo [0, 4], os pontos P = (x, y, k) dessa superfície formarão sobre o plano z = k a hipérbole y² - x² = 16.

Conclusão: a superfície é formada "empilhando" a hipérbole y² - x² = 16, começando no plano z = 0 e indo até z = 4.

A figura abaixo ilustra a superfície. Note que ela não é formada por uma revolução. Mais um detalhe: este tipo de superfície é conhecida como cilindro hiperbólico.

superficie.png (22.08 KiB) Exibido 2087 vezes