Obtenha os vértices B e C do triângulo equilátero ABC, sendo A = (1,1,0) e sabendo que o lado BC está contido na reta: (x,y,z) = t(0,1,-1).
Bom, pensei assim: eu já sei o vetor diretor de r, que é (1,1,0). Sei que cada ângulo interno vale 60 graus. Chamei o ponto B de (x,y,z). Como A = (1,1,0) então um vetor diretor da reta uqe passa por AB pode ser (x-1, y-1,z). Logo é só calcular o ângulo entre os vetores diretores usando a definição do produto interno. Mas o problema é que vai dar uma conta astronômica e eu não sei como eliminar as duas variáveis... eu não consigo encontrar uma outra relação tal que eu elimine x e y.


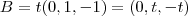
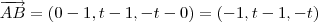
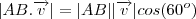
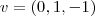

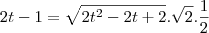
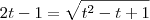
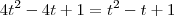
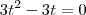
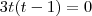


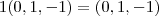
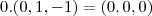
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)