KleinIll escreveu:Determine x e y para que os vetores
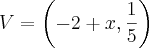
e
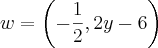
sejam iguais.
Tudo bem, temos que a divisão dos primeiros fatores de v e w é igual a divisão dos segundos. E o comprimento de v é igual ao de w.
Com estas afirmativas consegui duas equações.
O problema é que não há como resolver este sistema, cheguei em uma equação de quinto grau. Evidente que está errado, por isso peço a ajuda. Obrigado.
Para que dois vetores sejam iguais, eles precisam possuir: a mesma direção, o mesmo sentido e o mesmo comprimento (ou módulo).
Mas o que você fez foi o seguinte:
a) "(...) temos que a divisão dos primeiros fatores de v e w é igual a divisão dos segundos". Primeiro, aqui ao invés de dizer "fatores" você deveria dizer "coordenadas". Observado isso, o que você fez aqui foi dizer que os vetores v e w devem possuir a mesma direção.
b) "(...) E o comprimento de v é igual ao de w". Aqui você está claramente tratando sobre a igualdade entre os comprimentos (ou módulos).
Note então que você esqueceu de mais uma necessidade para que os vetores sejam iguais: eles devem possuir o mesmo sentido.
Resumindo então, para que os vetores
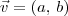
e

sejam iguais, devemos ter a = c e b = d.
Desse modo, considerando os vetores dados no exercício, para que eles sejam iguais, devemos ter:

Agora continue o exercício a partir daí.
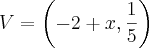 e
e 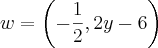 sejam iguais.
sejam iguais.

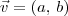 e
e  sejam iguais, devemos ter a = c e b = d.
sejam iguais, devemos ter a = c e b = d.
