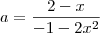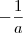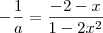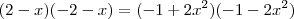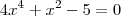por sauloandrade » Dom Out 28, 2012 21:08
por sauloandrade » Dom Out 28, 2012 21:08
Olá, boa noite, estou com o seguinte problema que eu não sei nem por onde começar, então queria que vocês podessem me dizer como proceder nessa questão.
Dado os pontos P1 (2;-1) e P2 (-2;1), determine todos os pontos S pertencente a parábola
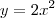
tal que P1S seja perpendicular a P2S.
Obrigado.
-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Out 28, 2012 21:44
por young_jedi » Dom Out 28, 2012 21:44
se traçarmos uma reta do ponto P1 ate o ponto S temos que o coeficiente angulara dessa reta sera
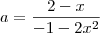
para que uma reta seja perpendicular a ela o seu coeficiente angular de ve ser igual
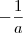
então pegando uma reta de P2 ate S teremos
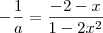
substituindo as expressões teremos
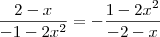
fazendo a multiplicação do sinal negativo e a multiplicação cruzada
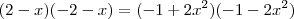

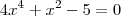
encontrando as raizes desta equação encontra-se os valores de x dos pontos procurados
qualquer duvida para encontrar as raizes ou sobre a resolução ate aqui, comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por sauloandrade » Dom Out 28, 2012 22:16
por sauloandrade » Dom Out 28, 2012 22:16
Obrigado cara, eu continuei o problema então cheguei em 2 pontos que foram (-1;2) e (1;2).
Nossa, era tão simples o problema, apenas multiplicar os coeficientes angulares e igualar a -1 e depois resolver o sistema. Novamente, obrigado. Abraços
-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema parabola
por Pedroa » Ter Mai 08, 2012 13:50
- 1 Respostas
- 1011 Exibições
- Última mensagem por joaofonseca

Ter Mai 08, 2012 17:25
Funções
-
- Problema com parábola
por Eusouopapao » Ter Out 09, 2012 13:28
- 0 Respostas
- 827 Exibições
- Última mensagem por Eusouopapao

Ter Out 09, 2012 13:28
Equações
-
- Problema envolvendo função
por marianacarvalhops » Sáb Mai 02, 2009 17:46
- 1 Respostas
- 4423 Exibições
- Última mensagem por Marcampucio

Sáb Mai 02, 2009 18:27
Funções
-
- Problema envolvendo equação
por ana tereza » Qui Set 10, 2009 23:47
- 3 Respostas
- 5750 Exibições
- Última mensagem por gabrielMAT

Qua Out 19, 2011 16:49
Sistemas de Equações
-
- Problema envolvendo capital
por Crist » Sex Mar 15, 2013 21:57
- 0 Respostas
- 1900 Exibições
- Última mensagem por Crist

Sex Mar 15, 2013 21:57
Equações Diferenciais Ordinárias e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
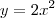 tal que P1S seja perpendicular a P2S.
tal que P1S seja perpendicular a P2S.
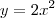 tal que P1S seja perpendicular a P2S.
tal que P1S seja perpendicular a P2S.