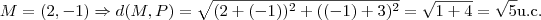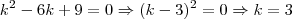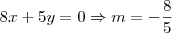por Luan A Zanatta » Dom Ago 08, 2010 18:14
por Luan A Zanatta » Dom Ago 08, 2010 18:14
Por Favor AJuda !
são exercicios de Matematica , uma meta !!
1)M é o ponto médio do segmento de extremos A(4,0) e B(0,-2). A media da distancia de M ao ponto P(-1,3) em unidades de comprimento é:
2)Se a reta de equação (k+5)x-(4-k²)y+k²-6k+9=0 passa pela origem , então seu coeficiente angular é:
-
Luan A Zanatta
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Ago 08, 2010 17:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agricola
- Andamento: cursando
 por MarceloFantini » Seg Ago 09, 2010 02:39
por MarceloFantini » Seg Ago 09, 2010 02:39
1)
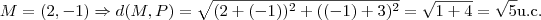
2) Se a reta passa pela origem, seu coeficiente linear é zero.
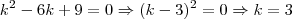
Logo:
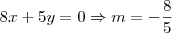
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com alguns exercícios
por Thiago Silveira » Seg Set 06, 2010 22:18
- 0 Respostas
- 5595 Exibições
- Última mensagem por Thiago Silveira

Seg Set 06, 2010 22:18
Funções
-
- Duvida em alguns exercícios de potenciação
por GiovaniF » Ter Mar 19, 2013 14:14
- 1 Respostas
- 1477 Exibições
- Última mensagem por timoteo

Ter Mar 19, 2013 21:51
Álgebra Elementar
-
- [Geometria Analitica] Duvidas em alguns exercicios
por Gustavo Reis » Qui Jun 27, 2013 13:50
- 1 Respostas
- 2216 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 29, 2013 10:22
Geometria Analítica
-
- [aneis e corpos] Ajuda sobre alguns problemas
por augusto0710 » Sex Nov 11, 2011 22:15
- 0 Respostas
- 8285 Exibições
- Última mensagem por augusto0710

Sex Nov 11, 2011 22:15
Álgebra Elementar
-
- [Esboço gráfico] Ajuda na construção de alguns esboços
por LeonardoIB » Sex Nov 15, 2013 18:54
- 0 Respostas
- 1188 Exibições
- Última mensagem por LeonardoIB

Sex Nov 15, 2013 18:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.